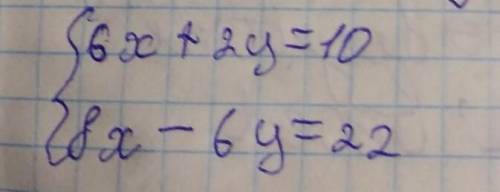
Сторона квадрата АВ = 8 см, ВР = ВЕ = 3 см. Поскольку КРЕМ - трапеция, то КМ параллельно РЕ, поэтому DK = DM = x.
Длина одного основания РЕ = 3*корень(2), длина другого КМ = х*корень 2, меняется от 8*корень 2 до 0.
Диагональ квадрата АС = BD = 8*корень(2).
Точки К и М в одном крайнем положении совпадают с А и С, в другом - обе совпадают с D, тогда трапеция вырождается в треугольник. Два крайних положения показаны на
Длина BN = PN = EN = 3*корень(2)/2. Длина DF = KF = MF = x*корень(2)/2. Длина OB = BD/2 = 4*корень(2)
Высота трапеции FN = BD - BN - DF = 8*корень(2) - 3*корень(2)/2 - x*корень(2)/2.
Площадь трапеции
S = (PE + KM) * FN / 2 = (3*корень(2) + х*корень(2)) * (8*корень(2) - 3*корень(2)/2 - x*корень(2)/2) / 2
S = корень(2) * (3 + x) * корень(2) * (8 - 3/2 - x/2) / 2 = (3 + x)(16 - 3 - x)/2 = (3 + x)(13 - x)/2 -> max
Неожиданно простая функция получилась. Дальше находим производную, и приравниваем к 0.
S ' = [ (13 - x) - (3 + x) ] / 2 = (10 - 2x) / 2 = 5 - x = 0
x = 5
ответ: точки К и М должны быть на расстоянии 5 см от точки D.
Объяснение:
Пусть по плану на выполнение заказа было дано х дней , тогда первая мастерская выполнила заказ за (х – 4) дня , а вторая за (х – 1) день . Первой мастерской нужно было сшить 600 рубашек, а второй 560. Следовательно, первая мастерская в день шила 600/(х-4) рубашки, а вторая 560/(х-1). Так как по условию задачи первая мастерская в день шила на 4 рубашки больше, чем вторая, то составим и решим уравнение:
600/(х-4)- 560/(х-1)=4 - умножим на (х-4)(х-1)
600(х-1)-560(х-4)=4(х-4)(х-1)
600х-600-560х+2240=4(х²-5х+4)
40х+1640=4х²-20х+16
4х²-60х-1624=0
х²-15х-406=0
По теореме, обратной теореме Виета х1=29; х2=-14- не подходит
600/(29-4)=24 - рубашки, шила первая мастерская в день
560/(29-1)=20 -рубашек, шила вторая мастерская в день
ответ: 24;20;
ответ: (2;-1)