
ответ: 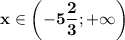
Объяснение:
Решить совокупность неравенств:
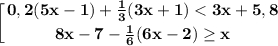
Решим каждое неравенство отдельно, а в ответ запишем все решения данных неравенств.
1. Решим первое неравенство.
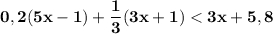
Раскроем скобки. Перенесем неизвестные влево, известные вправо. Не забываем при переносе через знак неравенства поменять знаки на противоположные.
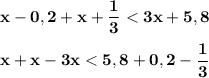
Приведем подобные члены:
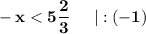
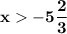
2. Аналогично решим второе неравенство.
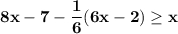
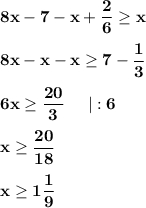
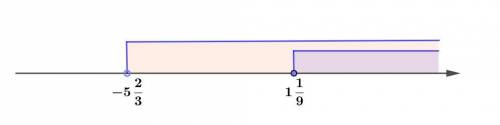
Отметим решения на числовой оси и объединим промежутки.
См. рис.
Получили ответ: 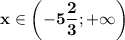
#SPJ1
1.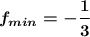
2. Функция возрастает на промежутке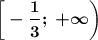
3. функция принимает не отрицательныe значения при
Объяснение:
f(x) = 3x² + 8x + 5
1. Найти меньшее значение функции.
График этой функции - парабола ветвями вверх.
Минимум функции достигается в вершине параболы.
Координата х₀ вершины по формуле
Тогда
2. Указать промежуток роста графика функции
Функция возрастает на промежутке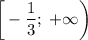
3. Найдите значение аргументов, при которых функция принимает не отрицательные значения
3x² + 8x + 5 ≥ 0
Сначала найдем нули функции
Приведем квадратное уравнение и применим теорему Виета
И теперь, поскольку это парабола ветвями вверх, неравенство
3x² + 8x + 5 ≥ 0 выполняется при