На изготовление 72 деталей первый рабочий тратит на 1 час меньше, чем второй рабочих на изготовление 50 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй Сколько деталей в час делает второй рабочий?
Объяснение: пусть первый тратит x-часов на изготовление 72 деталей ; тогда второй тратит x+1 -часов на изготовление 50 тогда скорость первого рабочего д/ч (деталей в час ) ; второго д/ч и нам известно что первый рабочий за час делает на 3 детали больше, чем второй то есть решим уравнение дальше выйдет квадратное уравнение выйдут корни второй корень отрицательный поэтому не берем тогда тогда второй рабочий за час изготовит деталей
1) Прямая имеет уравнение y = kx + b Точки M(2;4) и N(5;-2) принадлежат этой прямой, получаем систему уравнений 4 = k * 2 + b, -2 = k * 5 + b. Из первого уравнения b = 4 - 2k. Подставим во второе уравнение -2 = 5k + 4 - 2k => 3k = -6 => k = -2 => b = 4 - 2 * (-2) = 4 + 4 = 8 Уравнение MN: y = -2x + 8 Точки пересечения: с осью Ох: y = 0 => -2x + 8 = 0 => x = 4 (4;0) с осью Оу: x = 0 => y = -2 * 0 + 8 => y = 8 (0;8)
2) Так как график линейной функции проходит через начало координат, то ее уравнение y = k * x. Также она проходит через точку M(-2,5;4) 4 = k * (-2,5) => k = 4 : (-2,5) = -4/2,5 = -40/25 = -8/5 Получаем уравнение y = -8/5 * x. Для нахождения точек пересечения данной функции и прямой 3x - 2y - 16 = 0 решаем систему y = -8/5 * x, 3x - 2y - 16 = 0
y = -8/5 * x, 3x - 2 * (-8/5 * x) - 16 = 0
y = -8/5 * x, 3x + 16/5 * x = 16
y = -8/5 * x, 31/5 * x = 16 x = 16 * 5/31 = 80/31, y = -8/5 * 80/31 = -128/31 Получаем точку пересечения (80/31;-128/31)
Имеем нелинейную систему двух уравнений с двумя неизвестными.
Видимое сразу ограничение - только одно: у не равен 0 (у - в знаменателе). При дальнейшем анализе очевидно,что х также не равен 0, потому что, если подставить х в первое уравнение х +у = ху, получим 0 + у = 0*у, 0 + у = 0. Это равенство требует, чтобы у был равен 0, но это невозможно.
х +у = ху ху = х/у (умножим обе части уравнения на у/х)
уу = 1 у = - 1 или у = 1
Для каждого значения у находим х (подстановкой в первое уравнение):
1) у = - 1 х - 1 = х * (-1) х - 1 = - х х + х = 1 2х = 1 х = 1/2
2) у = 1 х + 1 = х *1 х + 1 = х Это равенство неверно при любом значении х.
ответ: 5 деталей за час сделает второй рабочий
Объяснение: пусть первый тратит x-часов на изготовление 72 деталей ; тогда второй тратит x+1 -часов на изготовление 50 тогда скорость первого рабочего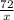
д/ч (деталей в час ) ; второго 
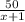д/ч и нам известно что первый рабочий за час делает на 3 детали больше, чем второй то есть 
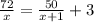решим уравнение 
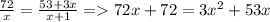дальше выйдет квадратное уравнение 
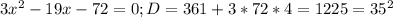выйдут корни 
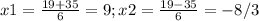второй корень отрицательный поэтому не берем тогда тогда второй рабочий за час изготовит 
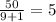деталей