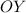Решите методом подстановки систему уравнений: x-3y=4 2x-y=3

Question

Алгебра: Решите методом подстановки систему уравнений: x-3y=4 2x-y=3

sofiazahhа · Accepted Answer

Точка пересечения этого графика с осью

равна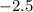

, когда

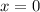, то есть эти точка должны пересекаться в этих точках .
Если первое касательная имеет вид
y=kx+b

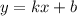то вторая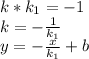 $k*k_{1}=-1\\
k=-\frac{1}{k_{1}}\\
y=-\frac{x}{k_{1}}+b\\\\
$
Видно что они должны быть симметричны относительно точки пересечения .
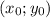Если $(x_{0};y_{0})$ это есть точка касательной к графику то у второй $(-x_{0};y_{0})$ .
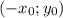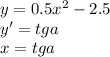
$y=0.5x^2-2.5\\ y'=tga\\ 
x=tga\\$
То есть в итоге получим прямоугольный треугольник . Заметим то что b<0

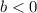так как график сам расположен ниже оси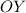

Рассмотрим треугольник который образовался с осью oX;oY

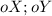, он прямоугольный по условию прямые перпендикулярные , пользуясь запись уравнения прямых получаем что они делятся на равные углы по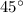 45а

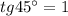
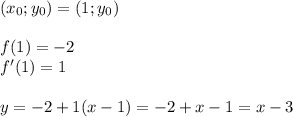
откуда $(x_{0};y_{0})=(1;y_{0})\\\\
f(1)=-2\\
f'(1)=1\\\\
 y=-2+1(x-1)=-2+x-1=x-3$
Вторая соответственно y=-x-3

MOGZ ответил

Решите методом подстановки систему уравнений:
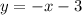
x-3y=4
2x-y=3