,
, a 
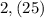
целая часть. У нас она равна 2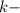
- количество цифр в периоде. У нас их 2
количество цифр до периода. У нас их 0
все цифры, включая период, в виде натурального числа. У нас это 25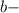
все цифры без периода в виде натурального числа. Их нет.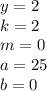
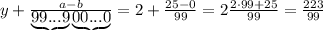
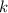подставляется количество 9, а под 
-количество нулей. У нас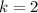 
, значит пишем две цифры 9, а 
, значит, нулей не пишем вообще. Между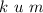 
не стоит знак умножения
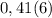
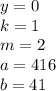
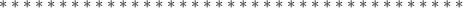
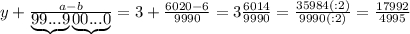
7,5
Объяснение:
(х²-у²)/5х² : (х²-2ху+у²)/25х= при х=2 у=1
В числителе первой дроби разность квадратов, развернуть, в числителе второй дроби квадрат разности, свернуть:
=[(x-y)(x+y)]/5x² : (x-y)²/25x=
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй, а знаменатель первой умножить на числитель второй.
=[(x-y)(x+y)*25х] : [5x²*(x-y)(x-y)]=
сокращение (x-y) и (x-y) на (x-y), 5 и 25 на 5, х и х² на х:
=5(х+у)/х(х-у)=
=5(2+1)/2(2-1)=
=15/2=7,5