Для того, чтобы определить точку максимума функции нужно проделать три шага.
1 шаг. Найти производную функции.
*ln(7)
2 шаг. Приравнять полученную производную к нулю.
Так как показательная функция никогда не может равняться нулю, приравниваем к нулю правый множитель.
3 шаг. Исследовать полученную точку на предмет максимума и минимума.
--------------------()---------------------> х
- -1 +
Вообще-то, у нас получилось, что это точка минимума, т.к. знак меняется с "-" на "+".
И, если внимательно посмотреть на функцию, то абсолютно очевидно, что у нее нет точки максимума, т.к. показательная функция с основанием больше 1 (7 > 1), следовательно она возрастающая, а в степени квадратичная функция с коэффициентом a > 0 (1 > 0), которая устремляется ветвями своей параболы в бесконечность и тоже является возрастающей.
Объяснение:
Для того, чтобы определить точку максимума функции нужно проделать три шага.
1 шаг. Найти производную функции.
2 шаг. Приравнять полученную производную к нулю.
Так как показательная функция никогда не может равняться нулю, приравниваем к нулю правый множитель.
3 шаг. Исследовать полученную точку на предмет максимума и минимума.
--------------------()---------------------> х
- -1 +
Вообще-то, у нас получилось, что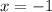 это точка минимума, т.к. знак меняется с "-" на "+".
это точка минимума, т.к. знак меняется с "-" на "+".
И, если внимательно посмотреть на функцию, то абсолютно очевидно, что у нее нет точки максимума, т.к. показательная функция с основанием больше 1 (7 > 1), следовательно она возрастающая, а в степени квадратичная функция с коэффициентом a > 0 (1 > 0), которая устремляется ветвями своей параболы в бесконечность и тоже является возрастающей.