ответ:Решение на фото
Объяснение:
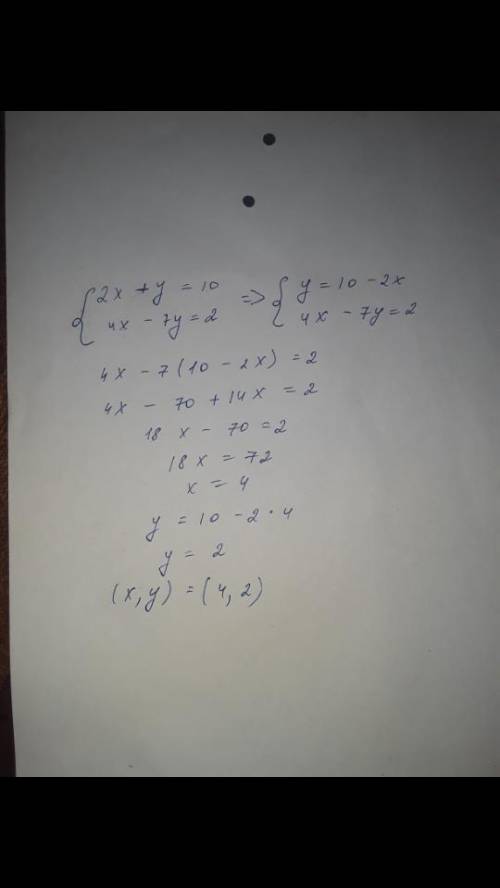
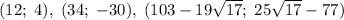
Объяснение:
![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt[6]{(x+y)^3(x-y)^2}=8](/tpl/images/1358/0734/79d4c.png)
Выполним преобразование:
![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt{x+y}\times\sqrt[3]{x-y}=8](/tpl/images/1358/0734/48821.png)
или ![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt{x+y}\times\sqrt[3]{x-y}=-8](/tpl/images/1358/0734/9c2ec.png)
Пусть ![\sqrt{x+y}=k,\;\sqrt[3]{x-y}=t](/tpl/images/1358/0734/e7517.png)
.
Тогда для 1-ого случая:
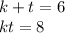
Заметим здесь теорему Виета (если не заметили, то можно просто решить эту систему).
Тогда:
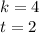
или
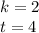
Замечу, что замену можно было не делать. Она дана для понимания. Можно было сразу написать то, что идет после слов обратная замена.
Обратная замена:
![1)\\\sqrt{x+y}=4\\\sqrt[3]{x-y}=2](/tpl/images/1358/0734/fbf65.png)
Первое уравнение можно возвести в квадрат, так как обе части его положительны:
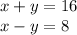
Очевиден прием решения: сложение.
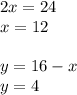
Получили пару чисел (12; 4).
![2)\\\sqrt{x+y}=2\\\sqrt[3]{x-y}=4\\\\x+y=4\\x-y=64\\\\2x=68\\x=34\\\\y=4-x\\y=-30](/tpl/images/1358/0734/7b359.png)
Получили пару (34; -30).
Для 2-ого случая:
![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt{x+y}\times\sqrt[3]{x-y}=-8\\\\\sqrt{x+y}=3+\sqrt{17}\\\sqrt[3]{x-y}=3-\sqrt{17}\\\\x+y=(3+\sqrt{17})^2\\x-y=(3-\sqrt{17})^3\\\\x=103-19\sqrt{17}\\y=25\sqrt{17}-77](/tpl/images/1358/0734/218c4.png)
Еще одна пара чисел: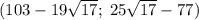 
Заметим, что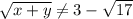 
, т.к. это число меньше 0.
Система уравнений решена!
Всего n=7+5=12 кроликов
По формуле классической вероятности
p=m/n=5/12 - вероятность вынуть черного кролика в одном испытании
q=7/12-вероятность вынуть белого кролика в одном испытании
Случайная величина Х – количество выбранных черных кроликов в четырех испытаниях
может принимать значения от 0 до 4
Х=0
означает, что ни разу не был выбран черный кролик.
Тогда вероятность этого события:
p₀=С⁰₄(5/12)⁰·(7/12)⁴
Х=1
означает, что один раз был выбран черный кролик.
Тогда вероятность этого события:
p₁=С¹₄(5/12)·(7/12)³
Х=2
означает, что два раза был выбран черный кролик.
Тогда вероятность этого события:
p₂=С²₄(5/12)²·(7/12)²
Х=3
означает, что три раза был выбран черный кролик.
Тогда вероятность этого события:
p₃=С³₄(5/12)³·(7/12)
Х=4
означает, что три раза был выбран черный кролик.
Тогда вероятность этого события:
p₄=С⁴₄(5/12)⁴·(7/12)⁰
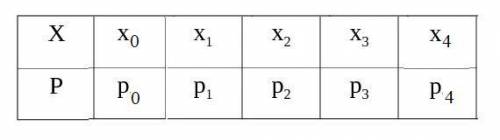
Закон распределения - таблица, в первой строке значения
Х от 0 до 4
во второй их вероятности.
(2;6)
Объяснение:
выразим y через x
подставим во второе уравнение первое, тогда получим
4x-10+2x=2
6x=12
x=2 ;
подставим х в первое уравнение
y=10-2*2
y=6