
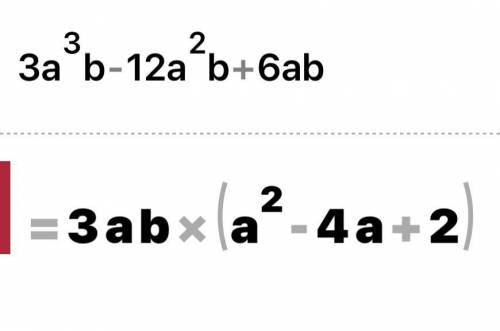
Объяснение:
задание 1
1) 3,2:2/7= 32/10*7/2= 11,2
2) 0,8*0,7=0,56
3) 11,2:0,56= 20
задание 2
х^3*(х^4)^3= х^3*х^12= х^15
а^6:а^7=а
задание 3
а) 5х-2х+6=6х
5х-6х-2х=-6
-3х=-6
х=2
б)6х-2х-5=6х-12
6х-5х-6х=5-12
-5х=-7
х= 1,4
задание 4
а) 3ав(а^2-4а+2)
б) (х+2)(х-1)
задание 5
а) 20а^5-5а^4+5а^2
б) 6с^2-15сх-2сх+5х^2=6с^2-17сх+5х^2
в)9а^2+12ав+4в^2
DenQ04a Ученый
б)
Строим таблицу, где первая колонка х, а вторая у.. .
ниже таблицы пишем
2х² + у = 4х - 3
2х² - 4х = -3 - у
При х=0, у=-3
х=1, у=-1
х=2, у=-3
х=3, у=-9
х=4, у=-19
(это пишем в таблицу)
Отмечаешь эти точки на координатной плоскости и соединяешь,
сначала имеет параболы, а от точки (2,-3) идет на низ прямая
в) xy = 8
y = 8/x
График - Гипербола
Строим таблицу
x≠0
x = -8, y = -1
x = -4, y = -2
x = -2, y = -4
x = -1, y = -8
x = 8, y = 1
x = 4, y = 2
x = 2, y = 4
x = 1, y = 8
Отмечаешь на координатной плоскости и проводишь Гиперболу.
При решении таких неравенств можно придерживаться следующей схемы.
1. Перенести все члены неравенства в левую часть.
2. Все члены неравенства в левой части привести к общему знаменателю, то есть неравенство записать в виде :
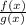
3. Найти значения х, при которых функция y= может менять свой знак. Это корни уравнений
4. Нанести найденные точки на числовую ось. Эти точки разбивают множество действительных чисел на промежутки, в каждом их которых функция будет знакопостоянной.
5. Определить знак в каждом промежутке, вычисляя, например, значение данного отношения в произвольной точке каждого промежутка.
6. Записать ответ, обращая особое внимание на граничные точки промежутков. При решении строгого неравенства >0 (<0) граничные точки в ответ не включаются. При решении нестрогого неравенства ? 0 ( ? 0), если точка является корнем знаменателя, то она не включается в ответ (даже если она одновременно является корнем числителя). Если же точка является корнем одного числителя, то она включается в ответ.