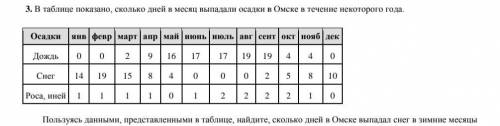
В течение всего года выпало ≈189мм осадков
Задать вопрос
Войти
АнонимГеометрия13 мая 17:10
треугольник MNP равнобедренный. один из углов равен 112 градусам. найти углы
ответ или решение1
Боброва Кира
Рассмотрим два возможный случая.
1 случай.
Данный угол величиной 112° является углом при вершине данного равнобедренного треугольника.
Тогда два других угла при основании будут равны между собой.
Обозначим через x величину этих углов.
Так как при сложении величин всех трех углов всякого треугольника в результате получается 180°, можем составить следующее уравнение:
х + х + 112 = 180,
решая которое, получаем:
2х + 112 = 180;
(2х + 112) / 2 = 180 / 2;
х + 56 = 90;
х = 90 - 56 = 34°.
2 случай.
Данный угол величиной 112° является углом при основании данного равнобедренного треугольника.
Тогда другой угол при основании также должен составлять 112°.
Так как суммы этих двух углов, равная 112 + 112 = 224° больше 180°, то такого треугольника не существует.
ответ: 112°, 54°, 54°.
найдём точку пересечения прямых
4y=3x ⇒ 12y=9x ⇒ 5x+12y=5x+9x=14x ⇒ 14x=10 ⇒ x = 5/7 ⇒ 4y=3·5/7=15/7 ⇒ y=15/28
найдём векторы нормали
-3x+4y=0 ⇒ n₁(-3;4)
5x+12y-10=0 ⇒ n₂(5;12)
Проверим, острый ли угол между n₁ и n₂ (равносильно n₁·n₂ > 0)
n₁·n₂=-3·5+4·12=-15+48 > 0
Находим единичные вектора нормали
n₁'=n₁/|n₁|=(-3;4)/√(3²+4²)=(-3/5;4/5)
n₂'=n₂/|n₂|=(5;12)/√(5²+12²)=(5/13;12/13)
Находим вектор нормали к биссектрисе острого угла между прямыми
n₃=n₁'+n₂'=(-14/65;112/65)
Другим вектором нормали будет n₃'=65/14 n₃=(-1;8)
Составляем уравнение биссектрисы по точке (5/7;15/28) и вектору нормали n₃
n₃'·(x,y)=n₃'·(5/7;15/28) ⇒ -x + 8y = -5/7 + 8 ·15/28 = 25 / 7, или
-7x + 56y = 25
другой возможный вариант решения, использовать тот факт, что любая точка биссектрисы равноудалена от двух данных прямых, и формулу расстояния от точки до прямой
|4y-3x|/√(4²+3²) = |5x+12y-10|/√(5²+12²)
13|4y-3x| = 5|5x+12y-10|
13(4y-3x) = ±5(5x+12y-10)
Один вариант знака даёт биссектрису острого угла, второй — биссектрису тупого угла, потом останется только разобраться, какой вариант к какой биссектрисе относится.
информация в таблице:
снег:
декабрь – 10
январь – 14
февраль – 19
10+14+19=43
ответ: 43 дня