Запишем формулу: P=m/n, где m – число исходов, благоприятствующих осуществлению события X, а n – число всех равновозможных элементарных исходов.
Для начала определим вероятность выпадения какого-либо числа при одном броске. Определённое число выпадает одно, а всего исходов может быть 6 (6 граней кубика). Значит, вероятность выпадения какого-либо числа = 1/6.
Так как бросков мы делаем 2, количество возможных результатов возводится во 2-ю степень, и вероятность выпадения какого-либо числа уже = 1 / 6 × 6 = 1/36. В последующем, мы будем домножать числитель на количество удовлетворяющих нас результатов.
Сумма выпавших очков делится на 5 при следующих результатах
1) 1 и 4 (=5)
2) 2 и 3 (=5)
3) 3 и 2 (=5)
4) 4 и 1 (=5)
5) 5 и 5 (=10)
Как видим, количество удовлетворяющих нас результатов = 5. Значит, вероятность выпадения числа, кратного 5 = 1 × 5 / 36 = 5/36 ≈ 0.139 = 13.9%
Сумма выпавших очков меньше, чем 8 при следующих результатах:
1) 1 и 1
2) 1 и 2
3) 1 и 3
4) 1 и 4
5) 1 и 5
6) 1 и 6
7) 2 и 1
8) 2 и 2
9) 2 и 3
10) 2 и 4
11) 2 и 5
12) 3 и 1
13) 3 и 2
14) 3 и 3
15) 3 и 4
16) 4 и 1
17) 4 и 2
18) 4 и 3
19) 5 и 1
20) 5 и 2
21) 6 и 1
Как видим, количество удовлетворяющих нас результатов = 21. Значит, вероятность выпадения чисел, сумма которых меньше 8 = 1 × 21 / 36 = 21/36 = 7/12 ≈ 0.583 = 58.3%
Произведение выпавших очков делится на 12 при следующих результатах:
1) 2 и 6
2) 3 и 4
3) 4 и 3
4) 6 и 2
Как видим, количество удовлетворяющих нас значений =4. Значит, вероятность выпадения чисел, произведение которых =12 составляет 1 × 4 / 36 = 4/36 = 1/9 ≈ 0,111 = 11,1%
Количество очков, выпавших в первый раз, и количество очков, выпавших
во второй раз, отличаются на 3 возможно при следующих результатах:
1) 1 и 4
2) 4 и 1
3) 2 и 5
4) 5 и 2
5) 3 и 6
6) 6 и 3
Как видим, количество удовлетворяющих нас результатов =6. Значит, вероятность выпадения чисел, количество очков которых, выпавших в первый раз, и количество очков, выпавших во второй раз, отличаются на 3 составляет 1 × 6 / 36 = 6/36 = 1/6 ≈ 0,166 = 16,6%
ответ: 1) 13.9%; 2) 58.3%; 3) 11,1%; 4) 16,6%.
Объяснение:
ВАРИАНТ 1.
Задание 1) у= х^2
Подставляем значения х и у в данную фунцкию:
A( 3:-9) , Где х=3, у= -9 (и последующие точки по аналогии)
Подставляем: -9=3^2
-9=9 - неверно, зн. точка не принадлежит графику функции у= х^2
B( 1;1)
у= х^2
1=1^2
1=1- верно, зн. точка принадлежит графику функции у= х^2
C(-1;-1)
у= х^2
-1=1 - неверно, зн. точка не принадлежит графику функции у= х^2
D ( -3;9)
у= х^2
9= 9 - верно, зн. точка принадлежит графику функции у= х^2
Задание 2)
а) х (нулевое) = -b\2a = 4\2= 2
у (нулевое) = у(х)=у(2) = 4-8+5= 1
(2;1)-вершина
б) х(нулевое) = 7\4
у(нулевое) = 2*49\16 - 7*7\4 + 9 = 49\8 - 49\4 + 9 = 49\8 - 96\8 +9 = = -49\8 + 9= 9 - 6 1\8 = 8 8\8 - 6 1\8 = 2 7\8
( 7\4; 2 7\8) - вершина
Задание 3.)
1) Пусть у = 0, тогда -2х^2 + 3х +2 = 0
D= 25
х 1 =- 1\2 х2 = 2
( -1\2 ;0) , (2;0) - точки пересечения параболы с осью ОХ
Пусть х=0 , тогда y=2
(0;2) - точка пересечения параболы с осью OY
4) у = х^2 - 2х -1
а) х (нулевое) = 2\2= 1
у(нулевое) = 1-2-1= -2
(1;-2) - вершина параболы
б) Пусть х=0, тогда у= -1
(0;-1) - точка пересечения с осью ОУ
в) х= -1, 2 ,3(подставляем значения х)
у= 2, -5, -4
Далее строим параболу по этим точкам. Находим, где функция возрастает, а где убывает.
Скорее всего в условии ошибка. Представляю исправленное условие.
Произведение равно нулю в том случае, когда хотя бы один из множителей обращается к нулю.
Если же в условии все в порядке, то решение следующее.
Решим это кубическое уравнение методом Кардано
Поделим обе части последнего уравнения на 4
Здесь коэффициенты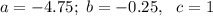
Поскольку S > 0 то кубическое уравнение имеет три действительных корня