Пусть х (км/ч) - скорость катера, тогда скорость катера по течению равна х+3 (км/ч), а против течения - х-3 (км/ч). Известно, что по течению катер проплыл 5 часов, в то время как против течения - 7 часов. Найдем пройденный путь для каждой ситуации:
S1 = (x+3)t1 - путь пройденный по течению, где t1 = 5ч
S2 = (x-3)t2 - путь пройденный против течения, где t2=7ч
Так как в обоих случаях пройден один и тот же путь, то S1 = S2. Приравняем их формулы и получим:
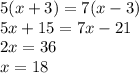
Таким образом, скорость катера в стоячей воде равна 18 км/ч.
По течению катер проплыл:
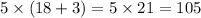
км
ответ:: S6 = 10,2
Объяснение:
1. Для определения суммы шести членов арифметической прогрессии необходимо узнать значение шестого ее члена и только тогда найти S6 по формуле
Sn = (a1 + an) : 2 * n.
2. Известна формула для энного члена арифметической прогрессии
аn = a1 + d *(n - 1).
3. Пользуясь этой формулой вычислим разность прогрессии d.
a4 = a1 + d * 3;
1,8 = 1,2 + 3 d;
d = (1,8 - 1,2) : 3 = 0,6 : 3 = 0,2.
4. Теперь найдем а6.
а6 = а1 + d * 5 = 1,2 + 0,2 * 5 = 1,2 + 1 = 2,2.
5. Отвечаем на во задачи
S6 = (a1 + a6) : 2 * 6 = (1,2 + 2,2) : 2 * 6 = 10,2.
а=4>0, следовательно наименьшее значение функция принимает
в точке, являющейся вершиной параболы.
Находим координаты вершины:
х(в)=-(-4).(2*4)=4/8=1/2
у(в)=4(1/2)²-4(1/2)+3=4/4-2+3=1+1=2 - наименьшее значение функции