(1 - Cos2x)*Sin2x = √3Sin²x
2Sin²x * Sin2x - √3Sin²x = 0
Sin²x(2Sin2x - √3) = 0
Sin²x = 0 2Sin2x - √3 = 0
Sinx = 0 Sin2x = √3/2
x = Пn, n э z 2x = (-1)^n*arcSin√3/2 + Пn, n э z
2x = (-1)^n*П/3 + Пn, n э z
x = (-1)^n*П/6 + Пn/2, n э z
Найдём корни из промежутка [-П, П/3] ,для этого будем поочерёдно подставлять вместо n целые числа, отрицательные, ноль и положительные и следить, чтобы не выйти из заданного промежутка.
- П, - 5П/6, - 2П/3, - П/3, - П/6, 0, П/6, П/3
посмотрим на левую и правую части
правая часть минимум при x=0 принимает значение 2
берем производную (x^2+2)' = 2x = 0 х=0
левая максимум при х=0 и принимает значение 2
тоже ищем экстремумы 1-x>=0 x<=1
x+1>=0 x>=-1
ОДЗ -1 <= x <=1
ищем экстремумы на границах
при х=-1 выражение =√(1-(-1)) + √(1-1) = √2
при х=1 выражение = √(1-1) + √(1+1) = √2
(√(1+х) + √(1-х))' = 1/2√(1+x) - 1/2√(1-x) = (√(1-x) - √(1+x))/2√(1-x)√(1+x)=0
√(1-x) = √(1+x)
2x = 0
x=0
√(1-0) + √(1+0) = 2
максимум при х=0
значит решение х=0
======
ну можно сделать замену
1-x=u
1+x=t
и решать систему
u+t=2
√u + √t = u² + t²
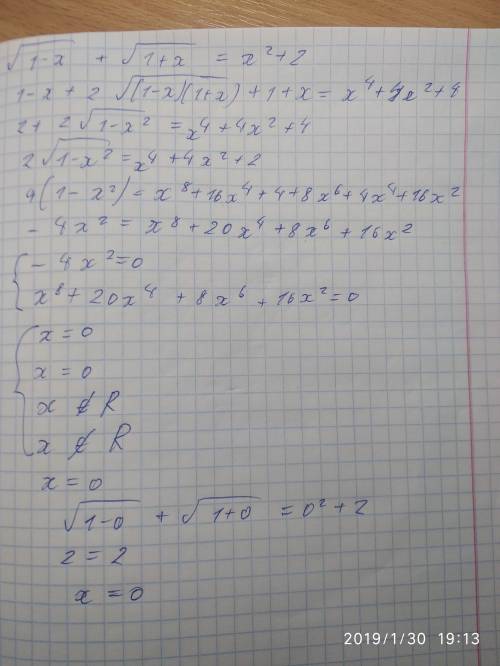 " />
" />
решение график фото сам решил