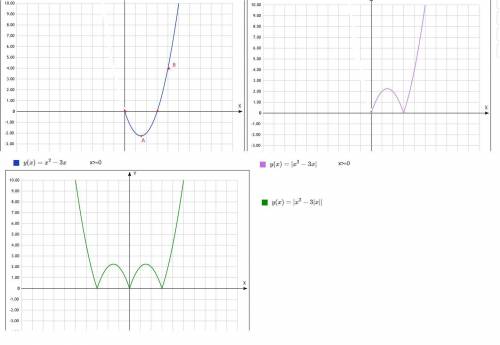
функция четная так как
y(-x)=|(-x)^2-3|-x||=|x^2-3|x|=y(x)
-значит ее график симметричен относительно оси ОУ и находится в первой и второй координатной четверти, так как у принимает только положительные значения и 0.
y=|x|*(|x|-3)
нули функции |x|=0 и |x|-3=0; |x|=3; x=-+3
а)построю график при положительном х и отражу его зеркально относительно ОУ
y=x^2-3x-ветвь параболы
ее вершина
x0=-b/(2a)=3/2=1.5
y(1.5)=1.5^2-3*1.5=2.25-4.5=-2.25
A(1.5;-2.25)-вершина
(3;0);(0;0)-нули функции
B(4;4)-четвертая точка
на рисунке это первый график y=x^2-3x для x>=0
б)отражаю зеркально отрицательную часть параболы относительно оси ОХ-это действие модуля, получаю на втором чертеже
y=|x^2-3x| при x>=0
в) полученный розовый график отражаю относительно оси ОУ-получаю график функции
y=|x^2-3|x||
Если ещё не изучено понятие производной, то решение может быть таким:
1. -2;
2. 3.
Объяснение:
1.Sn=6n-n^2
a1 = S1 = 6•1 - 1^2 = 5;
a1+a2 = S2 = 6•2 - 2^2 = 12 - 4 = 8;
a2 = S2 - S1 = 8 - 5 = 3.
Найдём d:
d = a2 - a3 = 3 - 5 = -2.
2. Sn=6n-n^2
Рассмотрим квадратичную функцию
у = 6х - х^2.
Графиком функции является парабола
у = - х^2 + 6х
Ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы. Найдём её координаты:
х вершины = -b/(2a) = -6/(-2) = 3.
y вершины = - 3^2 +6•3 = -9+18 = 9.
Наибольшего значения 9 функция у = - х^2 + 6х достигает при х = 3.
Так как 3 - натуральное число, то и наша функция Sn=6n-n^2, определённая только для натуральных n, достигает наибольшего значения 9 при n = 3.
Необходимо взять три первых члена прогрессии, чтобы их сумма была наибольшей и равной 9.
ответить на второй вопрос можно и по-прежнему другому:
Sn=6n-n^2
- n^2 + 6n = - (n^2 - 6n) = - (n^2 -2•n•3 + 9 - 9) = - ((n-3)^2 -9) = - (n-3)^2 + 9.
Так как слагаемое 9 постоянно, a - (n-3)^2 неположительно для любого n, то наибольшей сумма будет тогда, когда наибольшим будет первое слагаемое, т.е. когда - (n-3)^2 = 0, при n = 3.
В этом случае Sn = - (n-3)^2 + 9 = 0 + 9 = 9.