Решение
I х-3 I/3-х=-1
Найдем область допустимых значений
I х-3 I/3-х=-1 , х≠3
Упростим уравнение , используем перекрестное умножение
I х-3 I = -(3-х)
Переместим выражение в левую часть и сменим его знак
I х-3 I + (3-х) = 0
Когда перед выражением в скобках стоит знак + , тогда оно останется прежним
I х-3 I + 3-х = 0
Разделим уравнение
х-3+3-х=0 , х-3 ≥0
Решим уравнение + неравенство относительно х
х∈R , х≥3
Найдем пересечение множества решений и области допустимых значений
х∈[ 3 , +∞⟩
ответ
х∈⟨3 , +∞ ⟩
Пусть 100% - весь путь, который пройден со средней скоростью 50км/ч, тогда
х% - часть пути, которая пройдена со скоростью 45км/ч,
(100 - х)% - часть пути, которая пройдена со скоростью 60км/ч.
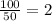 - все время движения;
- все время движения;
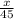 - время, движения со скоростью 45 км в час;
- время, движения со скоростью 45 км в час;
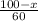 - время, движения со скоростью 60 км в час.
- время, движения со скоростью 60 км в час.
Уравнение.

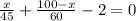
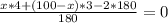
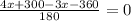

Дробь равна 0, если числитель равен нулю, значит:
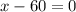
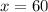
ответ: 60% пути он проехал со скоростью 45 км в час.
А можно и в частях:
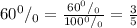
ответ:  пути он проехал со скоростью 45 км в час.
пути он проехал со скоростью 45 км в час.
Объяснение:
Сначала я всё перенесла в левую часть, чтобы справа остался ноль. Потом каждое неравенство приравняла к нулю, нашла иксы, отметила на координатной оси. Первое неравенство нестрогое, поэтому точка на координатной оси закрашенная. Второе неравенство наоборот строгое, поэтому точка незакрашенная. Дальше методом интервалов нашла промежуток у первого и второго неравенства. В ответ надо записать промежуток, удовлетворяющий обоим неравенствам, то есть тот промежуток, где штрихи пересекаются. ответ: ( 3,(3); + бесконечность)

решил фото задача уравнение