Объяснение:
16. Во сколько раз увеличится объем куба, если его ребра увеличить в два раза?
Решение.
Первоначальный объем куба V1=a³. (a - длина ребра).
Увеличим ребро в 2 раза. стало 2а
При этом объем стал V2=(2a)³=2³*a³=8a².
V2/v1=8a³/a³=8 раз.
ответ: 4) 8.
----------------------
17. В треугольнике ABC, AC = ВС = 365, AB = 24 . Найдите tg А.
Проведем высоту СН. Так как треугольник равнобедренный, то АН=ВН=24/2=12.
TgA=CH/AH - отношение противолежащего катета к прилежащему.
По т. Пифагора СН=√(АС²-АН²)=√(365²-12²)=364.8
tgA=364.8/12=30.4. нет правильного ответа.
-------------------
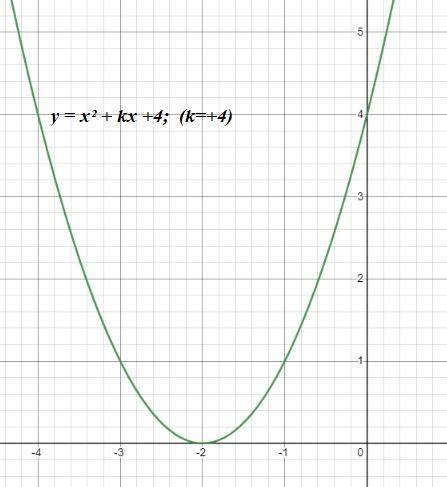
18. Найдите значение коэффициента k, при котором кривая
у = х² + kx +4 касается оси Ох;
ответ +4. (См. скриншот)
Объяснение:
Сначала нужно сделать так, чтобы коэффициенты при х и у были одинаковы.
Для этого умножим 1 уравнение на 3
{ 3x + 3y = 15
{ ax + 3y = c
Теперь, если a = 3 и с = 15, то система имеет бесконечно много решений,
потому что мы получаем два одинаковых уравнения.
{ 3x + 3y = 15
{ 3x + 3y = 15
То есть, по сути, одно уравнение с двумя неизвестными.
Если а = 3, и с не = 15, то решений нет, потому что мы получаем два противоречивых уравнения.
{ 3x + 3y = 15
{ 3x + 3y = 10
Во всех остальных случаях решение будет единственным. Например:
a = 8, c = 10
{ 3x + 3y = 15
{ 8x + 3y = 10
x = -1; y = 5 - x = 6