Задание № 1:
Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?
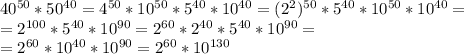
10^130 нас не интересует. Попробуем повозводить 2 в степень:
2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32
Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.
Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.
60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6
ОТВЕТ: 6
Решаем полное квадратное уравнение x^2 - 5x + 6 = 0 с нахождения дискриминанта.
Вспомним формулу для нахождения дискриминанта:
D = b^2 - 4ac;
Найдем дискриминант для заданного уравнения.
D = (-5)^2 - 4 * 1 * 6 = 25 - 24 = 1;
Дискриминант найден перейдем к нахождению корней.
x1 = (-b + √D)/2a = (5 + √1)/2 * 1 = (5 + 1)/2 = 6/2 = 3;
x2 = (-b - √D)/2a = (5 - √1)/2 * 1 = (5 - 1)/2 = 4/2 = 2;
Корни найдены. Сделаем проверку:
1) 3^2 - 5 * 3 + 6 = 0;
9 - 15 + 6 = 0;
0 = 0;
2) 2^2 - 5 * 2 + 6 = 0;
4 - 10 + 6 = 0;
0 = 0.
b)k<0,m>0
c)k>0,m<0
d)k<0,m<0
А проще провести прямые в рамках указанных углов,если:
концы проходят через 1 и 3 углы,то k>0,
концы проходят через 2 и 4 углы,то k<0,
m смотрим по оси ОУ если она выше 0 то m>0,иначе m<0.