Название
Дословно термин «тригонометрия» можно перевести как «измерение треугольников». Основным объектом изучения в рамках данного раздела науки на протяжении многих веков был прямоугольный треугольник, а точнее - взаимосвязь между величинами углов и длинами его сторон (сегодня с этого раздела начинается изучение тригонометрии с нуля). В жизни нередки ситуации, когда практически измерить все требуемые параметры объекта (или расстояние до объекта) невозможно, и тогда возникает необходимость недостающие данные получить посредством расчётов.
Например, в человек не мог измерить расстояние до космических объектов, а вот попытки эти расстояния рассчитать встречаются задолго до наступления нашей эры. Важнейшую роль играла тригонометрия и в навигации: обладая некоторыми знаниями, капитан всегда мог сориентироваться ночью по звездам и скорректировать курс.
Основные понятия
Для освоения тригонометрии с нуля требуется понять и запомнить несколько основных терминов.
Синус некоторого угла - это отношение противолежащего катета к гипотенузе. Уточним, что противолежащий катет - это сторона, лежащая напротив рассматриваемого нами угла. Таким образом, если угол составляет 30 градусов, синус этого угла всегда, при любом размере треугольника, будет равен ½. Косинус угла - это отношение прилежащего катета к гипотенузе.
Тангенс - это отношение противолежащего катета к прилежащему (либо, что то же самое, отношение синуса к косинусу). Котангенс - это единица, деленная на тангенс.
Стоит упомянуть и знаменитое число Пи (3,14…), которое представляет собой половину длины окружности с радиусом в одну единицу.
Популярные ошибки
Люди, изучающие тригонометрию с нуля, совершают ряд ошибок - в основном по невнимательности.
Во-первых, при решении задач по геометрии необходимо помнить, что использование синусов и косинусов возможно только в прямоугольном треугольнике. Случается, что учащийся «на автомате» принимает за гипотенузу самую длинную сторону треугольника и получает неверные результаты вычислений.
Во-вторых, поначалу легко перепутать значения синуса и косинуса для выбранного угла: напомним, что синус 30 градусов численно равен косинусу 60, и наоборот. При подстановке неверного числа все дальнейшие расчёты окажутся неверными.
В-третьих, пока задача полностью не решена, не стоит округлять какие бы то ни было значения, извлекать корни, записывать обыкновенную дробь в виде десятичной. Часто ученики стремятся получить в задаче по тригонометрии «красивое» число и сразу же извлекают корень из трёх, хотя ровно через одно действие этот корень можно будет сократить.
ответ: b < a < c
Пошаговое объяснение:
1.
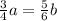
Рассмотрим это равенство. Домножим левую дробь на 6, правую - на 4, чтобы прийти к общему знаменателю:
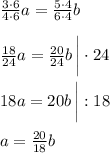
Получим равенство (1), откуда следует, что b < a.
2.
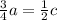
Рассмотрим это равенство. Домножим правую дробь на 2, чтобы прийти к общему знаменателю:
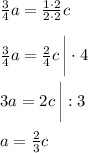
Получим равенство (2), откуда следует, что a < c.
3. Теперь сравним c и b. Из равенства (2) возьмем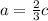 
и подставим в равенство (1):
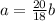
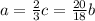
Домножим дробь при c на 6, чтобы прийти к общему знаменателю:
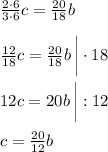
Откуда следует, что b < c.
Итак, мы получили следующее:
b < a
a < c
b < c
Откуда следует, что b < a < c.
ширина прямоугольника 2у
Площадь s=3x·2y=6ху
Длину увеличим в два раза, получим 3х·2=6х
Ширину уменьшим на 1 см, получим (2у-1)
Площадь S=6x·(2y-1)=12ху-6х
По условию S больше s на 12
Составляем уравнение
12ху-6х-6ху=12
6ху-6х=12
х·(у-1)=2
х=2
у-1=2 ⇒ у=3
ответ. х=2 ; у=3