Наибольшее значение функции g(x) на отрезке [0; 2] – 1
Объяснение:
1) Найдём производную данной функции:
g'(x) = 12x-12x^2
2) Найдём нули производной:
12x-12x^2=0
12x(1-x)=0
x1=0 x2=1
3) Определим "поведение" функции на отрезках [0; 1] и [1; 2]:
На отрезке [0; 1] функция возрастает
На отрезке [1; 2] функция убывает
Чтобы найти наибольшее/наименьшее значение первообразной функции, нужно подставить абсциссу точки максимума/минимума в первообразную функцию.
Точкa максимума функции g(x) – 1.
g(1) = 6-4-1 = 1
1) Квадратичная функция y=x^2 ; график функции парабола, ветви направлены вверх, с центром в О (0;0), проходит через точки: (1;1) и (-1;1), (2; 4) и (-2;4), (0; 1.5) и (-2; 1.5)
Линейная функция y=2x+3 ; график функции прямая, проходящая через точки (0;3) и (2;7)
По заданным точкам строим 2 графика.
2) Для нахождения точек пересечения приравняем y=y и найдем точки на абциссе (х):
2x+3=x^2;
x^2-2x-3=0
а=1
b=-2
c=-3
D= 4+12 = 16, х>0, х1,х2, 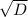 =4
=4
х1= (-b+4)/2a= 3
х2= (-b-4)/2a= -1
Подставим найденные x в уравнение y=x^2 и найдем ординату (у), y1=9; y2=1. Так точки пересечения двух графиков: (3;9) и (-1; 1).
Запишем ответ x= -1; 3
График получен из графика у=соsx сдвигом на (π/3) влево.
б) у=соsx возрастает на (-π+2πk;2πk), k∈Z
Решаем неравенство:
-π+2πk ≤ x+(π/3)≤2πk, k∈Z
у=сos(x+(π/3)) возрастает при
(-4π/3)+2πk ≤x≤(-π/3)+2πk, k∈Z .
у=соsx убывает на (2πk;π+2πk), k∈Z
Решаем неравенство:
2πk ≤ x+(π/3)≤π +2πk, k∈Z
у=сos(x+(π/3)) убывает при
(-π/3)+2πk ≤x≤(2π/3)+2πk, k∈Z .
в) Решаем уравнение
сos(x+(π/3))=0
x+(π/3)=(π/2)+πn, n∈Z;
x=(π/2)-(π/3)+πn, n∈Z;
x=(π/6)+πn, n∈Z.