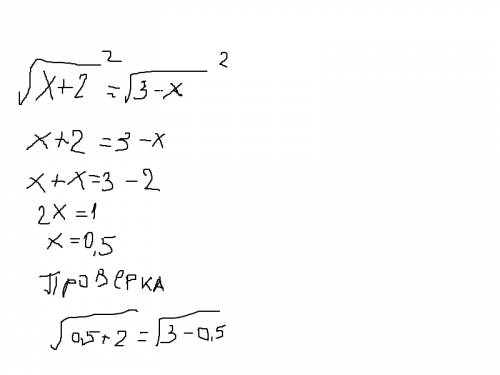
докажем сначала пункт б)
каждое натуральное число можна записать в виде 6k+1,6k+2, 6k+3, 6k+4, 6k+5, (то же самое что 6l-1), 6k+6, где k=0, или k - натуральное (так как при делении на 6 остатки могут быть 0,1,2,3,4,5)
числа вида 6k+2, 6k+4, 6k+6 четные поэтому делятся на 2, но но одно простое число больше 3 на 2 не делится, поэтому среди чисел этого вида нет простых
числа вида 6k+3=3*(2k+1) делятся на 3, но ни одно число большее 3, на 3 не делится, поэтому среди чисел данного вида нет протых чисел, поэтому простые числа находятся срди чисел вида р=6к+-1, к принадлежит N, что и требовалось доказать
теперь используя доказанный пункт б) докажем а)
р*р-1=(p-1)(p+1) - по формуле разности квадратов
рассмотрим два возможных случая
первый р=6k+1, к принадлежит N
тогда
р*р-1=(6k+1-1)(6k+1+1)=6k*(6k+2)=12k*(3k+1), а значит деится на 12
второй p=6k-1
p*p-1=(6k-1-1)(6k-1+1)=(6k-2)*6к=12к*(3к-1), а значит делится на 12.
Доказано
x и y - натуральные числа, значит числа y-x и y+x - целые.
y^2-x^2=123
(y-x)(y+x)=123
123 можно записать в произведение двух целіх чисел следующим образом
123=1*123=(-1)*(-123)=3*41=(-3)*(-41).
Значит получаем восемь систем уравнений
первая
y-x=1
y+x=123
y=(1+123)/2=62
x=(123-1)/2=61
(61;62) - подходит
вторая
y-x=123
y+x=1
x=(1-123)/2=-61 - не натуральное, не подходит
третья
y-x=-1
y+x=-123
не подходит так как сумма двух натуральных чисел число натуральное, а значит неотрицательное
четвертая
y-x=-123
y+x=-1
не подходит так как сумма двух натуральных чисел число натуральное, а значит неотрицательное
пятая
y-x=3
y+x=41
y=(41+3)/2=22
x=(41-3)/2=19
(19;22) - подходит
шестая
y-x=41
y+x=3
x=(3-41)/2=-19 - не подходит
седьмая
y-x=-3
y+x=-41
и восьмая
y-x=-41
y+x=-3
не подходят так как сумма двух натуральных чисел число натуральное, а значит неотрицательное
ответ: (19;22),(61;62)