1. нет; 2. 1) общего вида 2) общего вида 3) общего вида 3. 1) -1; 3 2) 1; -3 4) -1
Объяснение:
1. Если функция нечетная то произведение f(3)f(-3) не будет положительным.
2.
1)
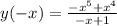
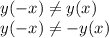
Это функция общего вида
2)
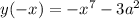
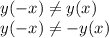
Это функция общего вида
3)
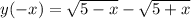
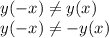
Это функция общего вида
3.
1)
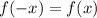
Значит
![min_{[2;4]}f(x)=min_{[-4;-2]}f(x)=-1\\max_{[2;4]}f(x)=max_{[-4;-2]}f(x)=3](/tpl/images/3904/3705/69e2d.png)
2)
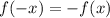
Значит
![min_{[2;4]}f(x)=-min_{[-4;-2]}f(x)=1\\max_{[2;4]}f(x)=-max_{[-4;-2]}f(x)=-3](/tpl/images/3904/3705/5cc0f.png)
4.
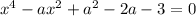
Это биквадратное уравнение. Делаем подстановку
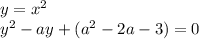
Уравнение будет иметь один корень, когда дискриминант равен 0
Но, поскольку х=±√у, то при любом положительном у мы получим два различных значения х. Одно значение х мы получим лишь в случае у=0. Тогда х=√0=0. Следовательно
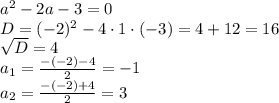
Делаем проверку:
1) а=-1
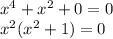
Имеется одно решение (т.к выражение в скобках никогда не будет равно 0)
2) а=3
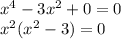
Здесь появляется второй корень. Значит, это значение не подходит.
Окончательно получаем решение: а=-1
x^2= -1
Квадратный корень из отрицательного числа не существует,значит
ответ: корней нет.
2)x^2 - 4x+4=0
D = b^2 - 4ac
D= 16 - 4*1*4= 16 -16 =0
D= 0
x1,2 = -b\2a = 4\2= 2
ответ: 2
3)x^2 - x=0
x(x - 1) =0
x= 0 или x -1 =0
x= 1
ответ: 0; 1
4)x^2+6x+5=0
D= b^2 - 4ac
D= 36 - 4*1*5= 36 - 20 = 16
x1 = -6+ 4 \ 2= -1
x2= -6-4\2 = -5
ответ: -5; -1.
5)x^ - 1=0
формула разности квадратов:
(x -1 ) * (x+1)= 0
x-1 =0 или х+1 =0
х1= 1 х2= -1
ответ: -1; 1.