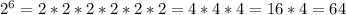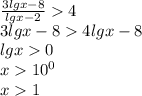
2x^-5x-12/2x+3
Чтобы сократить эту дробь, нужно разложить числитель и знаменатель на множители:
1) 2x^-5x-12 = а(х-х1)(х-х2); а - коэффициент перед х^2
Находим х1 и х2 через дискриминант:
D = b^2 - 4ac = 25 - (-96) = 121; √D = 11
x1 = (-b+√D)/2a = (5+11)/4 = 16/4 = 4
x2 = (-b-√D)/2a =(5-11)/4 = -6/4 = -3/2 = -1,5
Возвращаемся к формуле, подставляем полученные корни:
2x^-5x-12 = 2(х-4)(х+1,5)
2) 2х+3 = 2(х+1,5)
Возвращаемся к дроби, подставляем разложенные числитель и знаменатель:
2(х-4)(х+1,5)/2(х+1,5)
Сокращаем одинаковые множители и получаем ответ: х-4.
Объяснение:

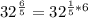
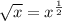
![\sqrt[3]{x} =x^{\frac{1}{3}}](/tpl/images/0503/0859/f093d.png)
![32^{ \frac{1}{5}} =\sqrt[5]{32}](/tpl/images/0503/0859/6c7d6.png)
![\sqrt[5]{32}=\sqrt[5]{2^{5}}](/tpl/images/0503/0859/ad486.png)
![\sqrt[5]{2^{5}}=2^{\frac{5}{5}}=2](/tpl/images/0503/0859/67bfa.png)