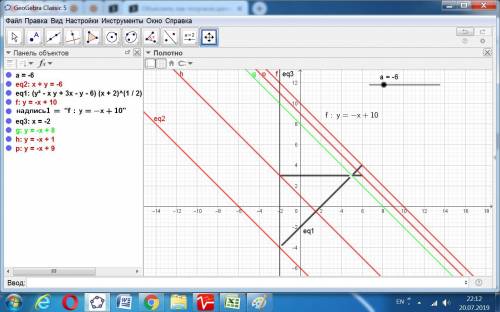
Приложенное решение верно.
Графически первая часть системы - это 2 отрезка прямых от х = -2 до х = 6 плюс прямая х = -2.
Произведём разложение первого множителя первого уравнения на множители сгруппировав:
у² - (х + 1)*у + (3х - 6) = 0
Имеем квадратное уравнение относительно "у".
Д = х² + 2х + 1 - 12х + 24 = х² - 10х + 25 = (х - 5)².
у1 = (х + 1 + х - 5)/2 = (2х - 4)/2 = х - 2.
у2 = (х + 1 - х + 5)/2 = 6/2 = 3.
Получили систему из двух прямых у = х - 2 и у = 3.
Но из за ограничений ОДЗ эти прямые представлены отрезками по аргументу от х = -2 до х = 6.
В сочетании с ещё одним решением числителя, полученного из корня (х = -2) графически первое уравнения системы представляет собой прямая х = -2 и 2 отрезка прямых у = х - 2, х = 3.
Теперь переходим к учёту двух уравнений системы.
Второе уравнение графически представляет собой прямую у = а - х, где параметр а представляет собой точку пересечения оси Оу.
При а = (-6...1], 8 и (9...10] система имеет 2 решения.
При а = 8 прямые первого уравнения пересекаются в одной точке, итого ещё с прямой х = -2 имеется 2 точки пересечения, что является решением системы.
При а = 1 и а = 10 решений системы тоже 2 и они входят в ответ.
Для начала вспомним что такое D(f) и E(f)
1 ) Множество всех значений, которые принимает аргумент функции, называется областью определения функции и обозначается D (f)
Т.е. Это все допустимые значения которые может принимать "х"
2) Множество всех значений, которые может принять зависимая переменная, называется областью значения функции и обозначается E (f)
Т.е. это все допустимые значений которые может принимать "у" в зависимости от "х"
Теперь рассмотрим нашу функцию
f(x)=x²+1
Есть ли такие "х" которые нельзя было бы подставить в нашу функцию и найти значение переменной "у"? - НЕТ
так что х∈(-∞;+∞)
теперь рассмотрим у
при х=0; у=0+1=1
при х=1; у=1+1=2
при х= -1; у=(-1)²+1=1+1=2
Значит все возможные значения у∈[1;+∞)
теперь поставим знаки
1) 3 ∈ D (f)
2) 0 ∈ D (f)
3) 1/2 ∉ E (f)
4) 1.01 ∈ E (f)
Объяснение:
(π/2 - arccosx)arccosx ≤ π²/16
-arccos²x + π/2 * arccosx - π²/16 ≤ 0
arccos²x - π/2 * arccosx + π²/16 ≥ 0
(arccosx - π/4)² ≥ 0 - верное неравенство.