a) 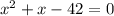
Ищем дискриминант:
D=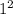 -4*1*(-42)=1-4*(-42)=1-(-4*42)=1-(-168)=1+168=169;
-4*1*(-42)=1-4*(-42)=1-(-4*42)=1-(-168)=1+168=169;
Дискриминант больше 0, уравнение имеет 2 корня: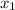 =
=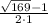 =(13-1)/2=12/2=6;
=(13-1)/2=12/2=6;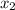 =
= 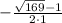 =(13-1)/2=12/2=6 =(-13-1)/2=-14/2=-7.
=(13-1)/2=12/2=6 =(-13-1)/2=-14/2=-7.
б) 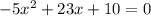
Ищем дискриминант:
D=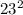 -4*(-5)*10=529-4*(-5)*10=529-(-4*5)*10=529-(-20)*10=529-(-20*10)=529-(-200)=529+200=729;
-4*(-5)*10=529-4*(-5)*10=529-(-4*5)*10=529-(-20)*10=529-(-20*10)=529-(-200)=529+200=729;
Дискриминант больше 0, уравнение имеет 2 корня: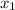 =
= 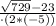 =(27-23)/(2*(-5))=4/(2*(-5))=4/(-2*5)=4/(-10)=-4/10=-0.4;
=(27-23)/(2*(-5))=4/(2*(-5))=4/(-2*5)=4/(-10)=-4/10=-0.4;
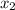 =
= 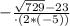 =-50/(2*(-5))=-50/(-2*5)=-50/(-10)=-(-50/10)=-(-5)=5.
=-50/(2*(-5))=-50/(-2*5)=-50/(-10)=-(-50/10)=-(-5)=5.
в) 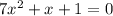
Ищем дискриминант:
D=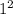 -4*7*1=1-4*7=1-28=-27;
-4*7*1=1-4*7=1-28=-27;
Дискриминант меньше 0, уравнение не имеет корней.
г) 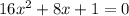
Ищем дискриминант:
D= 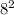 -4*16*1=64-4*16=64-64=0;
-4*16*1=64-4*16=64-64=0;
Дискриминант равен 0, уравнение имеет 1 корень:
X=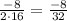 =-0.25
=-0.25
5sin²x + 3sinx × cosx - 4 = 0
5sin²x + 3sinx × cosx - 4×1 = 0
5sin²x + 3sinx × cosx - 4(sin²x + cos²x) = 0
5sin²x + 3sinx × cosx - 4sin²x - 4cos²x = 0
sin²x + 3sinx × cosx - 4cos²x = 0 | : cos²x
tg²x + 3tgx - 4 = 0
Пусть tgx = a, тогда:
a² + 3a - 4 = 0
D = 3² - 4×1×(-4) = 9 + 16 = 25
D>0, 2 корня
x₁ = -3+√25/2×1 = -3+5/2 = 2/2 = 1
x₂ = -3-√25/2×1 = -3-5/2 = -8/2 = -4
tgx = 1 или tgx = - 4
x₁ = π/4 + πn, n∈Z x₂ = arctg(-4) + πn, n∈Z
x₂ = - arctg 4 + πn, n∈Z
ответ: x₁ = π/4 + πn, n∈Z
x₂ = - arctg 4 + πn, n∈Z
Самое главное - не запутаться в буквах.
Найдем дискриминант этого уравнения.
Теперь думаем: при
Решим другое уравнение:
Итак, вот он ответ: при
Ради интереса можно сделать проверку, подставив вместо m единицу, и попробовать выделить полный квадрат.