Максимум в точке х = 
(для записи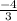 
)
Минимум в точке х = -1
Объяснение:
f(x)=2x^3+7x^2+8x+4
Область определения:
Х∈R
f(x)=2x^3+7x^2+8x+4, Х∈R
Определим производную f:
f(x) = 2x^3+7x^2+8x+4
f'(x) = d/dx (2x^3+7x^2+8x+4)
f'(x) = d/dx(2x^3) + d/dx(7x^2) + d/dx(8x) + d/dx(4)
f'(x) = 2*3x^2 + 7*2x+8+0
f'(x) = 6x^2+14x+8
f'(x) = 6x^2+14x+8, Х∈R
Представим f'(x) = 0
0=6x^2+14x+8
Решим ур-е относительно Х
6x^2+14x+8=0 | :2
3x^2+7x+4=0
D=b2-4ac = 7^2-4*3*4 = 1
x1,2= -b+-D/2a = -7+-1/2*3
x1= - 4/3
х2= -1
X∈(-∞;- 4/3)
X∈(- 4/3;-1)
max: - 4/3
min: -1
1) (8y + (3x + 5 y)= 8y + 3x + 5 y= 8у + 5 y + 3х= 13у + 3х
2) (15x + 2y) + ( 4x - 3y)= 15x + 2y + 4x - 3y= 15x + 4x +2y - 3y = 19x - y
3) (4a + 2) + (-a -1)= 4a + 2 -a -1= 4a - a + 2 -1 = 3a + 1
4) 0,4b + (1,2b - 0,1)=0,4b + 1,2b - 0,1 = 1,6b^2 - 0,1