Question

Y=-2sin x построить график функций и исследовать её.

Answer 1

1. Область определения функции — множество всех действительных чисел.

2. Множество значений функции:

Так как синус изменяется от -1 до 1, то оценивая в виде двойного неравенства, имеем

$-1\leqslant \sin x\leqslant1\\ -2\leqslant-2\sin x\leqslant2$

Множество значений функции y=-2sinx: отрезок [-2;2].

3. Функция периодическая с периодом T = 2π

4. Функция нечетная , так как y(-x) = 2sin x = -y(x)

5. Наибольшее значение, равное 2, при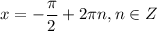 $x=-\dfrac{\pi}{2}+2\pi n,n \in Z$

Наименьшее значение, равное -2, при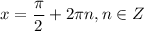 $x=\dfrac{\pi}{2}+2\pi n,n \in Z$

6. Функция возрастает на отрезке $\bigg[-\dfrac{3\pi}{2};-\dfrac{\pi}{2}\bigg]$ и на отрезках, получаемых сдвигами этого отрезка на $2\pi n,n \in Z$

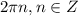
убывает на отрезке $\bigg[-\dfrac{\pi}{2};\dfrac{\pi}{2}\bigg]$ и на отрезках, получаемых сдвигами этого отрезка на $2\pi n,n \in Z$