Question

Дайте ответ с своим решением

Answer 1

Answer 2

Объяснение:

5) 5x - 2(2x-8)≥0

5x - 4x - 16 ≥0

x ≥ 16

ответ: x ∈ [ 16; + ∞)

6)$\left \{ {{2x+12 = 0 } \atop {x+5 < = 2}} \right.$

$\left \{ {{x = -6} \atop {x$

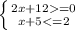
x ∈ [ -6; -3]

ответ: -3

7)

a) 16 - x^2 ≤0

(4-x)(4+x) ≤ 0

Нули функции:

4 - x = 0      4 + x = 0

x = 4            x = -4

(Тут строишь прямую, да и в принципе во всех предыдущих заданиях тоже)

(Будет что-то типа такого)

      -          -4        +          4        -      >x (методом интервалов находим нужный нам промежуток)

ответ: x ∈ ( -∞; -4]∪[4;+∞)

б)(x+3)(5x-10)> 0

нули ф.

x +3 = 0   5x - 10 = 0

x = -3      x = 2

       +          -3     -          2       +        >x (так же методом интервалов)

ответ: x ∈ ( - ∞; -3)∪(2; +∞)

9) 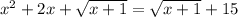$x^{2} + 2x + \sqrt{x+1} = \sqrt{x+1} +15$               О.Д.З

$x^{2} + 2x + \sqrt{x+1} - \sqrt{x+1} - 15 = 0$             x+1≥0                                                                  

x²+2x-15 = 0                                                  x ≥ -1

D = 2²-4*1*(-15) = 64

(можешь дальше дискриминантом решать)

По т. Виета:  

x(1) + x(2) = -b = -2 ;   x(1) = -5  - не уд. усл. О.Д.З

x(1)*x(2)=c = -15 ;        x(2) = 3

ответ: 3