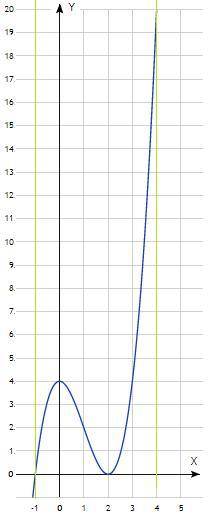
y = x³ - 3x² + 4
D(y) = R, кубическая функция непрерывна
Первая производная
y' = (x³ - 3x² + 4)' = 3x² - 6x
y' = 0; 3x² - 6x = 0; 3x(x - 2) = 0;
1) 3x = 0; x₁ = 0
2) x - 2 = 0; x₂ = 2
Знаки производной функции y'
++++++++++ [0] --------------- [2] +++++++++ > x
Функция возрастает на промежутках (-∞;0] и [2;+∞)
Функция убывает на промежутке [0;2]
x₁ = 0 - производная меняет знак с плюса на минус - точка максимума
x₂ = 2 - производная меняет знак с минуса на плюс - точка минимума
Значения на отрезке [-1; 4]
x = -1; y = (-1)³ - 3·(-1)² + 4 = -1 - 3 + 4 = 0
x = 0; y = 0³ - 3·0² + 4 = 4 - максимум функции
x = 2; y = 2³ - 3·2² + 4 = 8 - 12 + 4 = 0 - минимум функции
x = 4; y = 4³ - 3·4² + 4 = 64 - 48 + 4 = 20
Наибольшее значение функции в точке x=4, y=20
Наименьшие значение функции в точках x=-1 и x=2, y=0
1) 5sinx =3 ⇔ sinx = 0,6 ⇒ x = (-1)ⁿarcsin(0,6) +πn , n ∈ ℤ .
2) 1 - 2sinx = 0⇔ sinx = 1/2 ⇒ x = (-1)ⁿπ/6 +πn , n ∈ ℤ .
3) 4sinx +5 =0 ⇔ sinx = -1,25 ⇒ x ∈ ∅ . не имеет решения | sinx | ≤ 1
4) 2sin(3x +π/3) + √3 =0 ⇔sin(3x +π/3) = -(√3) /2 ⇒
3x+ π/3 = (-1) ⁿ⁻¹ π/3 + πn ⇔ (совокупность _ИЛИ )
[ 3x+ π/3 = - π/3 + π*2k ; 3x+ π/3 = π/3 + π*(2k+1) , k ∈ ℤ ⇔
[ x = - 2π/9 + (2π/3)k ; x= (π/3)(2k+1) , k ∈ ℤ
5) 12sin(x/4 -π/6) -12 =0 ⇔sin(x/4 -π/6) =1 ⇒ x/4 -π/6 =π/2 +2πk ,k ∈ ℤ ⇔
x = 8π/3 +8πk ,k ∈ ℤ
6) (2sin4x - 4)(2sinx+1) =0 ⇔ (sin4x -2)(sinx +1/2) = 0 ||sin4x ≠2 || ⇔
sinx +1/2 =0 ⇔sinx = -(1/2) ⇒ x =(-1) ⁿ⁻¹ *(π/6) + πn , n ∈ ℤ
7) sin(x/2)cos(x/3) -cos(x/2)sin(x/3) =0⇔sin(x/2 - x/3) =0 ⇔sin(x/6) =0 ⇒
x/6 =πn , n ∈ ℤ ≡ x = 6πn , n ∈ ℤ
8) 4sin3x*cos3x - √2 =0 ⇔ 2sin(2*3x) - √2 =0 ⇔sin(6x) =(√2)/2 ⇔
6x =π/4 +πn , n∈ℤ ⇔ x = π/24 +(π/4)*n , n∈ℤ
Объяснение:
упростите выражение
а)-3а+7в-8а-2в=-11a+5b;
б)с⁸/с³*с=c⁸/c⁴=c⁸⁻⁴=c⁴;
в)-3 а⁵в²*(7а³)2=-3*7*2a⁸b²=42a⁸b².