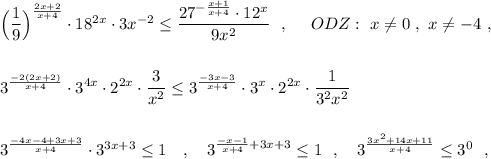
![a=31\ \ \to \ \ \dfrac{3x^2+14x+11}{x+4}\leq 0\ \ ,\ \ \ \dfrac{3(x+1)(x+\frac{11}{3})}{x+4}\leq 0\ \ ,\\\\\\znaki:\ \ ---(-4)+++[\ \frac{11}{3}\ ]---[-1\ ]+++\\\\\\x\in (-\infty ;-4\ )\cup [\ \frac{11}{3}\ ;-1\ ]](/tpl/images/2002/5491/97228.png)

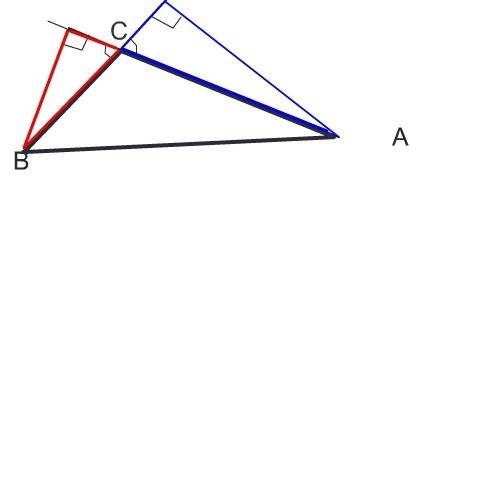
Сделайте рисунок и сразу увидите решение.
В каждом из этих треугольников один угол прямой, так как высота - это перпендикуляр, а еще по одному равны как вертикальные. Следовательно, третий угол в них тоже равен.
Эти треугольники подобны по равенству их трех углов.
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
А прямоугольные треугольники подобны, если острый угол одного треугольника равен острому углу другого. Здесь острые углы - вертикальные и равны.