
Биномиальное распределение стремится к нормальному при больших n
По условию
р = 0.9
соответственно
q = 1- p = 0.1
Математическое ожидание
М= np= 1000 * 0.9 = 900
Дисперсия
D= npq = 1000*0.9*0.1= 90
Сигма = √D= 3√10 = ~9.5
Мы рассматриваем интервал от центра распределения 900 до 940 - это больше чем четыре сигмы.
В этом случае в табличку нормального распределения можно даже не заглядывать, хвостик за четыремя сигмами очень малюсенький, пятый знак после запятой.
Половина всей выборки до 900 , половина после.
ответ
Вероятность равна ~0.5
3)a)cos^2a/sin^a+cos^2a-1/sin^2a=
приведу все к общему знаменателю sin^2a
=(cos^2+cos^2a*sin^2a-1)/sin^2a=
разложу 1=cos^2a+sin^2a
=((cos^2a+cos^2a*sin^2a-cos^2a-sin^2a)/sin^2a=
=(cos^2a*sin^2a-sin^2a)/sin^2a=sin^2a(cos^2a-1)/sin^2a=
=cos^2a-1=cos^2a-cos^2a-sin^2a=-sin^2a
б)sin5a-sina=2*sin((5a-a)/2)*cos((5a+a)/2)=2sin2a*cos3a
сам пример
2sin2a*cos3a/(2cos3a)*ctga-1=sin2a*ctga-1=
=2sina*cosa*cosa/sina-1=2cos^2a-1=2cos^2a-sin^2a-cos^2a=
=cos^2a-sin^2a=cos2a
4) ctg^2a=cos^2a/sin^2a подставлю в тождество слева
cos^2a/sin^2-1=(cos^2a-sin^2a)/sin^a=cos2a/sin^2a
5)cos74+cos16=2cos((74+16)/2)*cos((74-16)/2)=2cos45*cos29
x=45
1
2
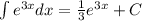
10.1
2
3
4
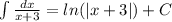
11.1
2
3
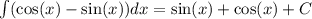
12.1
2
3
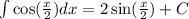
13.1
2
141
2
151
2
3
16.1
2
3