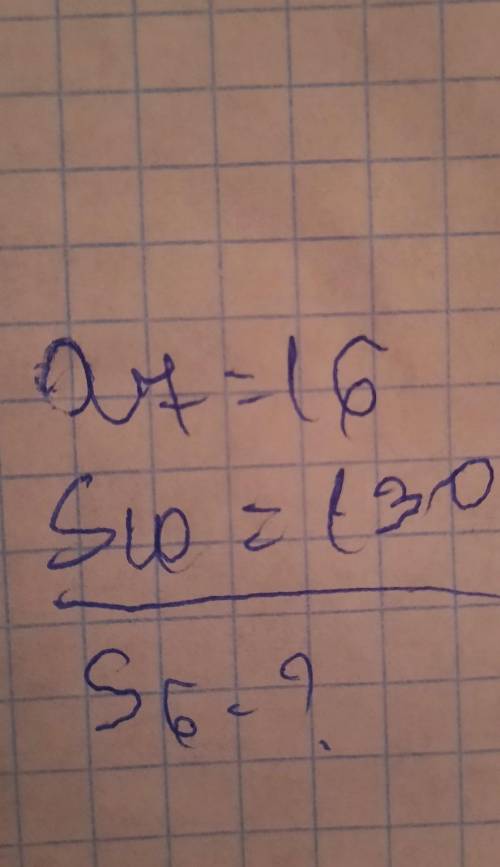
а) модуль числа а это само число а, если оно взято со знаком + и число !а!=-а, если а число отрицательное, т.е. взято со знаком -. Отсюда можно сделать вывод что модуль никогда не может быть равен отрицательному числу, абсолятное значение всегда положительно, поэтому единственное число, удоволтворяющее !x!=-x это 0, поэтому под буквой а можешь отметить только 0
б) Во втором случае этому уравнению будет эквивалентна система уравнений вида
x+2=x+2 - тождественно верно
x+2=-(x+2)-решаем
x+2=-x-2
x+x+2+2=0
2x+4=0
2x=-4
x=-2
Значит все точки числовой прямой начиная с x=-2 и в положительнную сторону будут удоволетворять уравнению, отсюда ответ будет вся числовая прямая начиная с -2 и больше
Сначала найдём значения параметра k. Приравняем оба графика, поскольку они пересекаются, а затем уже наложим дополнительные условия.
kx = -x² - 1
x² + kx + 1 = 0
Графики будут иметь одну общую точку тогда и только тогда, когда данное квадратное уравнение будет иметь 1 корень. Найдём те k, при которых данное квадратное уравнение имеет 1 корень. Если квадратное уравнение имеет 1 корень, то его дискриминант строго равен 0.
D = b² - 4ac = k² - 4
D = 0 k² - 4 = 0
k² = 4
k1 = 2; k2 = -2
Значит, при k = 2 и при k = -2 оба графика буцдут иметь ровно одну общую точку.
Теперь построим такие прямые. Надо построить y = -x² - 1 и прямые y = 2x, y = -2x. Скажу просто на всякий случай, что обе прямые будут симметричны относительно оси ox. Сейчас пришлю рисунок с построением(надеюсь, вы понимаете, как строятся эти прямые). Построение лишь приближённое и грубое, но видно, что обе прямые касаются параболы в какой-то точке, то есть фактически имеет с ней одну единственную точку.