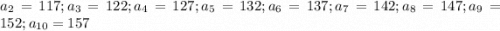Для начала разберем, что такое арифметическая прогрессия. Это такая последовательность чисел, где каждое число, начиная со второго равно предыдущему, сложенному с одним и тем же числом, то есть с разностью арифметической прогрессии. Наглядно это выглядит так:
.
Также существует формула - го члена арифметической прогрессии:
Где - разность арифметической прогрессии.
Из формулы выше, найдем разность арифметической прогрессии. Зная из условия, что , после данного числа идет девять неизвестных чисел и последним числом будет .
Подставляем наши значения:
- нашли разность арифметической прогрессии. Тогда по первой формуле мы без проблем можем найти все 9 неизвестных чисел:
Мы нашли все девять неизвестных членов арифметической прогрессии:
Можно решить путем составления системы уравнений. обозначим через х - число деталей в день 1 рабочего, а через у - количество дней. тогда для второго рабочего это будет х+5 и у-1 составим систему { ху=100 (х+5)(у-1)=100 преобразуя эту систему, получим у=(х+5)/5. далее в выражение ху=100 подставим значение у. получим квадратное уравнение x^2+5x-500=0. корнями этого уравнения будут х1=-25, х2=20. выбираем 20. столько изготавливает в день первый рабочий.
Объяснение:
Для начала разберем, что такое арифметическая прогрессия. Это такая последовательность чисел, где каждое число, начиная со второго равно предыдущему, сложенному с одним и тем же числом, то есть с разностью арифметической прогрессии. Наглядно это выглядит так:
Также существует формула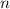 - го члена арифметической прогрессии:
- го члена арифметической прогрессии:
Где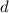 - разность арифметической прогрессии.
- разность арифметической прогрессии.
Из формулы выше, найдем разность арифметической прогрессии. Зная из условия, что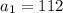 , после данного числа идет девять неизвестных чисел и последним числом будет
, после данного числа идет девять неизвестных чисел и последним числом будет 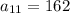 .
.
Подставляем наши значения:
Мы нашли все девять неизвестных членов арифметической прогрессии: