912.
Сначало всё обозначим:
скорость лодки х ;
скорость лодки против чтения х-4 ;
время пути по реке 20/х-4 ;
время пути по озеру 14/х.
Разница между тем и другим временем 1 час по условию. Составляем уравнение:
20/х-4 - 14/х = 1
Приводим к общему знаменателю, перемножаем, получаем квадратное уравнение:
х^2 - 10х - 56 = 0
По формуле квадратных корней находим
х1 = - 4
отбрасываем, отрицательной скорости не бывает,
х2 = 14
принимаем, это собственная скорость лодки. Скорость лодки против течения 14 - 4 = 10 (км/ч)
914.
(знаки это дробь)
Так как скорость не может принимать отрицательное значение, следовательно искомый ответ : 40.
ответ : Токарь должен был обрабатывать 40 деталей в час по плану.
915.
Решение.
Пусть х изделий бригада должна была изготовить в 1 день по плану
(120/х) дней - бригада должна работать
(х+2) - изделия
Бригада изготовляла фактически в 1 день 120/(х+2) дней - бригада работала фактически.
А так как, по условию задачи, бригада закончила работу на 3 дня раньше срока, то составим уравнение:
120/х - 120/(х+2) = 3
120(х+2) - 120х = 3х(х+2)
120х+240 - 120х - 3х² - 6х = 0
3х² + 6х - 240 = 0
х² + 2х - 80 = 0
D = 4 + 4 × 1 × 80 = 324
x¹ = (-2 - 18)/2 = - 10 < 0 не удовлетворяет условию задачи
х² = (-2 + 18)/2 = 8
8 - изделий бригада рабочих изготовляла в 1 день по плану.
ответ : 8 изделий.
Нуу вроде всё)
1) Найдем нулю нашей функции. Для чего разложим на множители формулу, которой она задана, с введения новых вс членов.
Из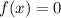
следует:
а)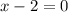
, отсюда 
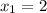- нуль функции
б)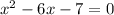
, 
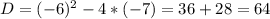, отсюда
Итак, функция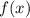
обращается в нуль в точках 
, 
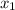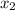и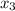 
2) Найдем возможные точки экстремума нашей функции. Для чего найдем производную функции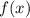
:
Разложим квадратный трехчлен, стоящий в правой части (1), на целые множители. Для чего найдем дискриминант этого квадратного трехчлена:
Тогда с (2) выражение (1) примет вид метода интервалов найдем промежутки, на которых производная функции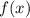
принимает положительные и отрицательные значения:
а)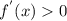
при x принадлежащем объединению промежутков
(-бесконечности; 1/3)U(5; +бесконечности )
б)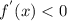
при x принадлежащем промежутку (1/3; 5)
Известно, что промежутки, на которых производная функции положительна, являются промежутками возрастания функции!
На промежутках, где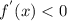
, функция убывает!
Поскольку при переходе через точку x=1/3 производная меняет знак с плюса на минус, то эта точка - точка максимума
Поскольку при переходе через точку x=5 производная меняет знак с минуса на плюс, то эта точка - точка минимума. Итак,