У андроксуса было 8 патронов в обойме.В новом патче ему убрали 25% от его обоймы. Сколько в новом у него было патронов в обойме?

👇

Увидеть ответ

Ответ:

kotletka223

28.06.2021

Объяснение:

8 - 25% = 8 - 2*2 = 8 -2 = 6

4,4(2 оценок)

Ответ:

Lapatkoanna

28.06.2021

1) 8 : 100 • 25 = 6 (п) осталось в обойме

4,7(54 оценок)

Открыть все ответы

Ответ:

ДжулиТян

28.06.2021

Объяснение: y=f(x)

1) D(f) . Область определения - это множество значений "х", на котором задаётся функция . Если задан график, то, чтобы определить ООФ, надо все точки, лежащие на графике, спроектировать на ось ОХ. Полученное множество и будет ООФ.

Все точки данного графика проектируются на все точки оси ОХ. То есть получаем множество всех действительных чисел.

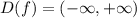
$D(f)=(-\infty ,+\infty )$

P.S. Множество значений функции E(f) - это значения, которые может принимать переменная "у" . Чтобы найти E(f) по графику, надо проектировать точки графика на ось ОУ. Для изображённой функции E(f)=[ -2; 2 ] .

2) Точка пересечения с осью ОХ - (0,0). Эта же точка (0,0)- точка пересечения с осью ОУ.

3) Функция возрастает на промежутке [ -3; 3 ] , х∈[ -3;3 ]. Если вести карандашом по графику от точки (-3,-2) до точки (3,2), то карандаш движется вверх, функция возрастает.

Промежутков убывания нет (нет участков, на которых карандаш движется вниз) .

P.S. Есть промежутки постоянства функции (где карандаш движется по прямой), это участки х∈(-∞ -3] и х∈[ 3,+∞).

4) Нули функции - это значения "х", при которых "у" обращается в 0 . Для изображённой функции - это х=0 (см. пункт 2). То есть f(0)=0.

5) Наибольшее значение функции - это у=2 , наименьшее значение функции - это у= -2 ( cм. пункт 1 , P.S. )

4,6(12 оценок)

Ответ:

mrtwesor

28.06.2021

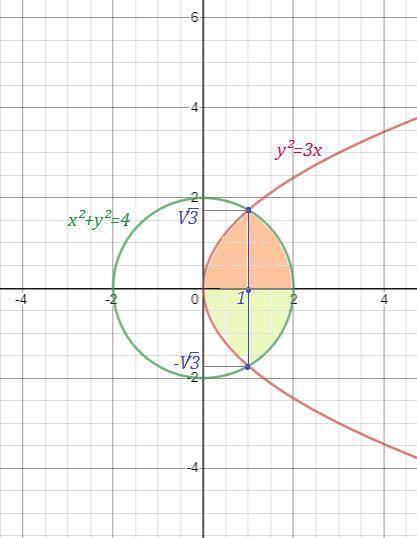
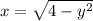$x=\sqrt{4-y^2}$ - это правая полуокружность от окружности 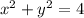x^2+y^2=4 с центром в точке (0,0) и R=2 , выразим 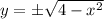$y=\pm \sqrt{4-x^2}$ , причём для 1-ой четверти знак перед корнем (+) , а для 4-ой четверти знак (-) .

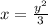$x=\frac{y^2}{3}$ - это парабола , ветви которой направлены вправо, вершина в точке (0,0) . Выразим y: 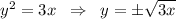$y^2=3x\; \; \Rightarrow \; \; y=\pm \sqrt{3x}$ , причём знак (+) перед корнем для 1-ой четверти, а знак (-) для 4-ой четверти.

Область симметричная относительно оси ОХ. Поэтому можно подсчитать площадь одной половины, а затем удвоить её.

Найдём точки пересечения окружности и параболы.

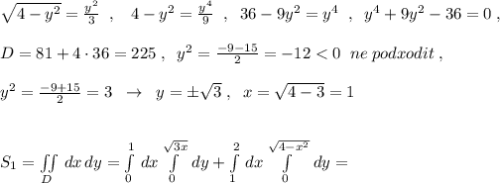
$\sqrt{4-y^2}=\frac{y^2}{3}\; \; ,\; \; \; 4-y^2=\frac{y^4}{9}\; \; ,\; \; 36-9y^2=y^4\; \; ,\; \; y^4+9y^2-36=0\; ,\\\\D=81+4\cdot 36=225\; ,\; \; y^2=\frac{-9-15}{2}=-12$

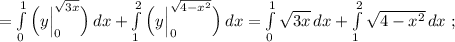
$=\int\limits^1_0\Big (y\Big |_0^{\sqrt{3x}}\Big)\, dx+\int \limits _1^2\Big (y\Big |_0^{\sqrt{4-x^2}}\Big)\, dx=\int\limits^1_0\sqrt{3x}\, dx+\int\limits^2_1\sqrt{4-x^2}\, dx\; ;$

$Q=\int \sqrt{4-x^2}\, dx\\\\Q=\int \frac{4-x^2}{\sqrt{4-x^2}}\, dx=4\int \frac{dx}{\sqrt{4-x^2}}-\int \frac{x\, \cdot \, x\, dx}{\sqrt{4-x^2}}=\Big[\; u=x\; ,\; du=dx\; ,\\\\dv=\frac{x\, dx}{\sqrt{4-x^2}}\; ,\; v=-\frac{1}{2}\cdot 2\sqrt{4-x^2}=-\sqrt{4-x^2}\; ,\; \int u\, dv=uv-\int v\, du\; \Big]=\\\\=4\cdot arcsin\frac{x}{2}-\Big(-x\sqrt{4-x^2}+\int \sqrt{4-x^2}\, dx\Big)=\\\\=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}-Q\; \Rightarrow \; \; Q=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}-Q\; ,$

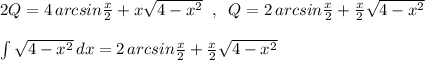
$2Q=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}\; \; ,\; \; Q=2\, arcsin\frac{x}{2}+\frac{x}{2}\sqrt{4-x^2}\\\\\int \sqrt{4-x^2}\, dx=2\, arcsin\frac{x}{2}+\frac{x}{2}\sqrt{4-x^2}$

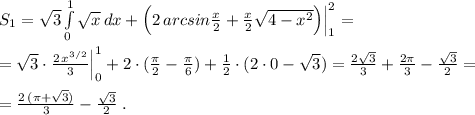
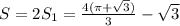
$S_1=\sqrt3\int \limits _0^1\sqrt{x}\, dx+\Big(2\, arcsin\frac{x}{2}+\frac{x}{2}\sqrt{4-x^2}\Big)\Big|_1^2=\\\\=\sqrt3\cdot \frac{2\, x^{3/2}}{3}\Big|_0^1+2\cdot (\frac{\pi}{2}-\frac{\pi}{6})+\frac{1}{2}\cdot (2\cdot 0-\sqrt3)=\frac{2\sqrt3}{3}+\frac{2\pi }{3}-\frac{\sqrt3}{2}=\\\\=\frac{2\, (\pi +\sqrt3)}{3}-\frac{\sqrt3}{2}\; .$