х - цифра десятков (0<x<9)
у - цифра единиц (0<y<9)
По условию сумма цифр двузначного числа равна 8, получаем первое уравнение:
х+у=8
(10х+у) - данное число
(10у+х) - число, записанное теми же цифрами, но в обратном порядке.
По условию если данное число разделить на число, записанное теми же цифрами,но в обратном порядке, то в частном получится 4 в остатке 3.
(10х+у) : (10у+х) = 4(ост. 3)
Получим второе уравнение:
10х+у = 4·(10у+х)+3
Упростим его:
10х+у=40у+4х+3
6х-39у = 3
2х-13у = 1
Решаем систему:
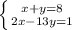
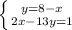

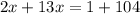
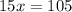
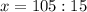
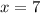

7 - цифра десятков
1 - цифра единиц
71 - данное число
ответ: 71
1,2 - первая пара
3,4 - вторая пара
5,6 - третья пара
7,8 - четвертая пара
1) В каждой паре четное число равно 2*N, где N - номер пары.
Значит 10-е четное число будет находиться в 10 паре, и чтобы его найти, надо 2 умножить на 10. 2*10 = 20.
99-е четное число будет находиться в 99 паре, и чтобы его найти, надо 2 умножить на 99. 2*99 = 198.
2) В каждой паре нечетное число равно 2*N-1, где N - номер пары.
Значит 12-е нечетное число будет находиться в 12 паре, оно равно
2*12 - 1 = 23.
77-е нечетное число будет находиться в 77 паре, оно равно
2*77 - 1 = 153.