Построим сперва прямую y=x-1. Прямая y=x, как известно, — это прямая, проходящая через начало координат и идущая вправо-вверх под углом в 45° (можешь проверить несколько точек и убедиться). А чтобы получить y=x-1, надо сместить прямую y=x на одну клетку вниз.
Нам подходят все точки ниже прямой (ведь у них координата y меньше, чем у соответствующих точек прямой; а у соответствующих точек прямой координата как раз x-1). Очевидно, сама построенная прямая не входит в нужную нам область (ведь нам надо y<x-1, а на самой прямой y=x-1). Поэтому её надо нарисовать пунктиром (обычно обозначают так).
ответ: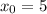 .
.
Угловой коэффициент прямой у=2х-2 равен k=2 . Если касательная параллельна этой прямой или совпадает с ней , то их угловые коэффициенты равны.
Угловой коэффициент касательной к графику функции y=f(x) равен значению производной в точке касания, то есть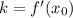 .
.
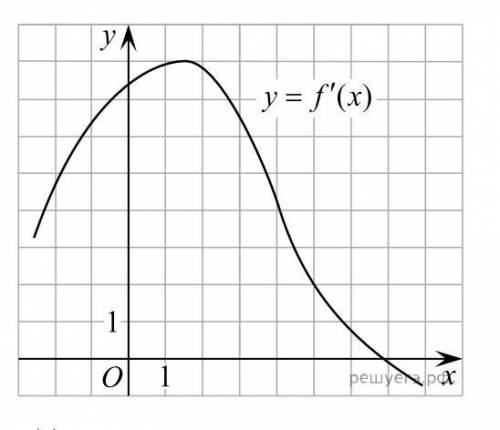
На оси ординат находим значение у=2, проводим прямую, параллельную оси ОХ, и находим на графике функции точку М - точку пересечения графика с прямой у=2.
Далее Находим абсциссу точки М . Это и будет абсцисса точки, в которой касательная к графику функции y=f(x) параллельна прямой y=2x-2 или совпадает с ней.
Координаты точки М(5;2) , значит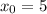 .
.