Без взятия производных для определения наибольшего и наименьшего значений функции приходится строить график этой функции.
График функции 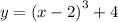 можно получить из графика
можно получить из графика 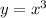 следующим образом:
следующим образом:
1. График 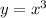 сдвигаем по оси аргументов на 2 единицы вправо (так как -2). Либо ось аргументов сдвигаем влево. Смотри рисунок.
сдвигаем по оси аргументов на 2 единицы вправо (так как -2). Либо ось аргументов сдвигаем влево. Смотри рисунок.
2. Полученный график y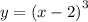 сдвигаем по оси значений функции на 4 единицы вверх (так как +4). Либо ось значений сдвигаем относительно графика вниз.
сдвигаем по оси значений функции на 4 единицы вверх (так как +4). Либо ось значений сдвигаем относительно графика вниз.
Полученный график функции 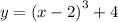 показан самым жирным и самым синим на рисунке.
показан самым жирным и самым синим на рисунке.
Из графика видим, что на отрезке ![\left[0;3\right]](/tpl/images/0129/5065/c1b3c.png) рассматриваемая функция монотонно возрастает и наименьшим значением будет значение в точке начала отрезка, а наибольшим — в точке конца.
рассматриваемая функция монотонно возрастает и наименьшим значением будет значение в точке начала отрезка, а наибольшим — в точке конца.
Итак, ответ.
![min|_{\left[0;3\right]} y(x) = y(0) = \left(0 - 2\right)^3 + 4 = -8 + 4 = -4](/tpl/images/0129/5065/af09b.png)
![max|_{\left[0;3\right]} y(x) = y(3) = \left(3 - 2\right)^3 + 4 = 1 + 4 = 5](/tpl/images/0129/5065/8238e.png)
<> Здравствуйте, Xonkil! <>
• ответ:
y = cos(3χ) + cos(3χ)
y = 4cos(2χ)
• Пошаговое Объяснение:
|
| • Корень (n/6+kn/3, 0), k ∈ ℤ
|
| • Область определения x ∈ ℝ
|
| • Минимум (n/3+2kn/3, -2), k ∈ ℤ
|
| • Максимум (2kn/3, 2), k ∈ ℤ
|
| • Пересечение с осью ординат (0,2)
– – – – –
|
| • Корень (n/4+kn/2, 0), k ∈ ℤ
|
| • Область определения х ∈ ℝ
|
| • Минимум (n/2+kn, -4), k ∈ ℤ
|
| • Максимум (kn, 4), k ∈ ℤ
|
| • Пересечение с осью ординат (0, 4)
[ P. s. Ниже указана схема к данной задаче. Если что, она принадлежит мне и чертила я её в специальном приложении. ]
<> С уважением решить! Буду благодарна за не слишком краткий ответ(те чтобы было понятно откуда идёт след">
(см. объяснение)
Объяснение:
Пусть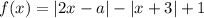 .
.
Тогда нужно, чтобы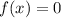 имело единственное решение.
имело единственное решение.
Заметим, что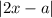 играет решающую роль в определении поведения функции (ее возрастания/убывания). Если он открывается со знаком +, то функция возрастает, иначе убывает.
играет решающую роль в определении поведения функции (ее возрастания/убывания). Если он открывается со знаком +, то функция возрастает, иначе убывает.
Тогда промежуток убывания:![\left(-\infty;\;\dfrac{a}{2}\right]](/tpl/images/2004/3019/c9b16.png) .
.
Промежуток возрастания: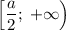 .
.
Единственное решение будет, если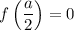 .
.
Получили уравнение:
Значит при данных значениях параметра a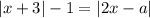 имеет единственное решение.
имеет единственное решение.
Бесконечное множество решений будет, если левая и правая части совпадают (то есть графики наложатся). Но это невозможно, так как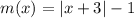 более широкий (прямой угол), чем
более широкий (прямой угол), чем 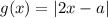 (острый угол) и величина угла от параметра никак не зависит.
(острый угол) и величина угла от параметра никак не зависит.
Задание выполнено!
Комментарий:
Можно было решать задачу, строя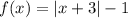 и
и 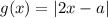 . Первый график имеет фиксированное положение, а второй бегает влево-вправо. Тогда тоже легко сделать требуемый вывод.
. Первый график имеет фиксированное положение, а второй бегает влево-вправо. Тогда тоже легко сделать требуемый вывод.