1)8х²-12х+36=0
D=(-(-12))²-4×8×36=144-1152=-1008
D<0, решения нет.
3х²+32+80=0
3x²+112=0|÷3
x²+37,33=0
x²=-37,33 Решения нет, так как любое число в квадрате не может быть отрицательным.
2)3x^2 + 32x + 80 = 0;
D = b^2 - 4ac, где:
ах^2 + bx + c = 0;
D = 32^2 - 4 * 3 * 80 = 1024 - 12 * 80 = 1024 - 960 = 64.
Сейчас найдем корень квадратный из дискриминанта:
√D = √64 = 8.
Найдем корни уравнения:
х1 = (-b + √D)/2a = (-32 + 8)/2 * 3 = -24/6 = -3 - первый корень уравнения.
х1 = (-b - √D)/2a = (-32 - 8)/2 * 3 = -40/6 = -6,67 - второй корень уравнения.
3)12y^2+16y-3=0
D1= 8^2-12*(-3)=64+36=100
y1=-8+10=2
y2=-8-10=-18
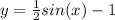
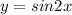
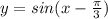

(9ˣ-2·3ˣ⁺¹)²₊14(9ˣ₋2·3ˣ⁺¹)≥0
(9ˣ-6·3ˣ)²₊14(9ˣ₋6·3ˣ)≥0
9ˣ₋6·3ˣ = z
z² + 14z ≥ 0
z(z + 14) ≥ 0
[-14] [0]
1. z ≤ - 14
9ˣ₋6·3ˣ ≤ -14
9ˣ₋6·3ˣ +14 ≤ 0
9ˣ = 3²ˣ
D = 36 - 4*14 < 0
Ветви вверх
D < 0
решений нет
2. z ≥ 0
9ˣ₋6·3ˣ ≥ 0
3ˣ(3ˣ - 6) ≥ 0
3ˣ - 6 ≥ 0
x ≥ log(3) 6
ответ x ≥ log(3) 6