Объяснение:
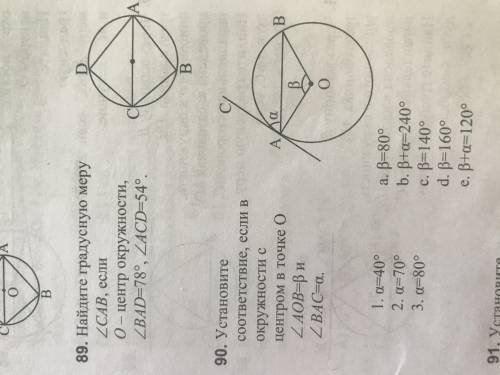
№89
∠СDA = 90°, т.к. Вписанный угол, опирающийся на диаметр, является прямым углом. Следовательно,
ΔСDA - прямоугольный. Сумма всех углов = 180°. Значит,
∠DAC = 180° - 90° - 54° = 36°
∠ВАD = ∠DAC +∠САВ, откуда
∠САВ = ∠ВАD - ∠DAC = 78°-36° =42°
∠САВ = 42°
№ 90
1) Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами, т.е.
∠α = ½ ∪АВ, откуда
∪АВ = 2∠∝
α = 40° → β = 80° (1а ) → α + β =120° (1с )
α = 70° → β = 140° (2с) α + β =210°
α = 80° → β = 160° (3d) α + β = 240° (3b)
ответ: 1а, 1 с
2с
3d, 3b
у наим = -1
Объяснение:
Исследуем функцию
у = (8 - х) · е⁹ ⁻ ˣ на промежутке [3;10]
Производная функции
y' = (-1) · е⁹ ⁻ ˣ + (8 - x) · е⁹ ⁻ ˣ · (-1)
y' = е⁹ ⁻ ˣ · (-1 - 8 + x)
y' = е⁹ ⁻ ˣ · (х - 9)
Найдём точки экстремума
у' = 0
е⁹ ⁻ ˣ · (х - 9) = 0
С учётом того, что е⁹ ⁻ ˣ > 0 при любых значениях х, получим
х - 9 = 0
х = 9 - точка экстремума
При х < 9 y' < 0 и у ↓ (убывает)
При х > 9 y' > 0 и у ↑ (возрастает)
При х = 9 производная у' меняет знак с - на +, поэтому
х = 9 - точка минимума
Точка минимума принадлежит промежутку [3;10], поэтому на границах промежутка значения функции будут больше, чем в точке минимума, и именно в точке минимума значение функции будет наименьшим
у наим = у(9) = (8 - 9) · е⁹⁻⁹ = -1 · е⁰ = -1
Відповідь:
Пояснення: