Question

решить номера:5, 6.
Заранее

Answer 1

$5)\ \ a^2-14a+49=(a-7)^2\\\\25y^2+10y+1=(5y+1)^2\\\\100a^2-180ab+81b^2=(10a-9b)^2\\\\16m^2+49n^2-56mn=(4m-7n)^2\\\\x^{10}-6x^5b+9b^2=(x^5-3b)^2\\\\36n^6+m^{12}+12m^3n^6=(6n^3+m^6)^2$

$6)\ \ x^2-25=(x-5)(x+5)\\\\36-16y^2=(6-4y)(6+4y)\\\\4x^2-81y^2=(2x-9y)(2x+9y)\\\\0,09y^2-1,21p^2=(0,3y-1,1p)(0,3y+1,1p)\\\\a^2b^2-\frac{16}{9}=(ab-\frac{4}{3})(ab+\frac{4}{3})\\\\a^8-x^4=(a^4-x^2)(a^4+x^2)\\\\0,04b^4-a^{12}=(0,2b^2-a^6)(0,2b^2+a^6)\\\\-1+a^6b^4=a^6b^4-1=(a^3b^2-1)(a^3b^2+1)$

Answer 2

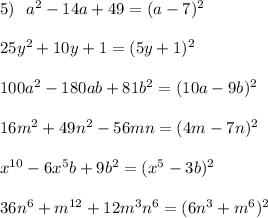
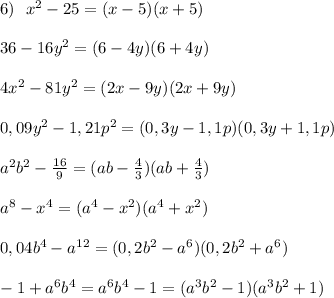
Объяснение:

Задание 5:

Общая для всех формула: a^2 ± 2ab + b^2 = (a±b)^2

1) a^2 - 14a + 49 = (a - 7)^2

2) 25y^2 + 10y + 1 = (5y+1)^2

3) 100a^2 - 180ab + 81b^2 = (10a - 9b)^2

4) 16m^2 + 49n^2 - 56mn = (4m - 7n)^2

5) x^10 - 6x^5b + 9b^2 = (x^5 - 3b)^2

6) 36m^6 + n^12 + 12m^3n^6 = (6m^3 + n^6)^2

Задание 6:

Общая для всех формула: a^2 - b^2 = (a + b)(a - b)

1) x^2 - 25 = (x + 5)(x - 5)

2) 36 - 16y^2 = (6 + 4y)(6 - 4y)

3) 4x^2 - 81y^2 = (2x + 9y)(2x - 9y)

4) 0.09y^2 - 1.21p^2 = (0.3y + 1.1p)(0.3y - 1.1p)

5) a^2b^2 - 16/9 = (ab + 4/3)(ab - 4/3)

6) a^8 - x^4 = (a^4 + x^2)(a^4 - x^2)

7) 0.04b^4 - a^12 = (0.2b^2 + a^6)(0.2b^2 - a^6)

8) -1 + a^6b^4 = (1 + a^3b^2)(1 - a^3b^2)

(Отметье как лучший ответ)