Question

разобраться с этими 2 заданиями, ответы обведены . Объясните ​

Answer 1

Объяснение:

1 . 5)   y = x² - 6x - 4 ;  вітки параболи  напрямлені вгору , тому  а > 0 ;

графік перетинає вісь Оу  у точці ( 0 ; - 4 ) , тому вільний член  с = - 4 ;

D > 0 , тому парабола перетинає у двох точках . Для вершини параболи

х₀  = - b/2a = 6/2 = 3 > 0 .

2 .  2)  y = - ( x + 2 )² + 3 ; даний графік одержаний із графіка функції

у = - х²  ( вітки параболи  напрямлені вниз ) перенесенням  вздовж

осі Ох  на 2 одиниці вліво і  на 3 одиниці вгору . Точку перетину графіка із віссю Оу знаходимо , підставивши у дане рівняння  х = 0

( у = - ( 0 + 2 )² + 3 = - 4 + 3 = - 1 .

Answer 2

Объяснение:

Рис.1

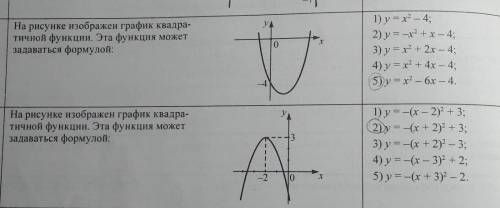
Квпдпатичная ф-ция задается формулой

$\\ y = a {x}^{2} + bx + c \\ a 0 \: ветви \: \: параболы \: \: вверх \\ a < 0 \: ветви \: \: параболы \: \: вниз$

1 шаг▪︎смотри куда направлены ветви параболы, в нашем случае вверх => а>0 => исключаем второй вариант ответа2 шаг▪︎сразу обратим внимание в формуле на с - это свободный член, он показыет в какой точке наш график пересекает ось Оу, здесь в точке -4 => подходят все варианты3 шаг▪︎сразу исключим 1 вариант ответа, т.к. четко видно что нули функции, т.е. точки на оси Ох -2 и 2 => должны быть симметричны оси Оу, у нас четко видно что несимметричны4 шаг▪︎вершина параболы

$x_{0} = \frac{ - b}{2a}$

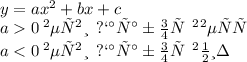
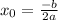
подставляем значения 3 варианта ответа и получаем х(0) = -1 не подходит, т.к. по рисунку видно, что

х(0) > 0

Так же не подходит и 4 вариант ответа: х(0) = -2

5 шаг▪︎наш ответ 5 вариант, т.к. все предылущие мы исключили

Рис.2

▪︎наша парабола задана формулой:

у = (х-m) + n

m - показывает куда смещается вершина пораболы по оси Ох

(х-m) вправо

(х-m) вправо(х+m) влево

n - показывает куда смещается вершина пораболы по оси Оу

+n вверх

-n вниз

ветви опущены вниз => а<0, => перед скобкой должен быть вершина параболы (-2;3) => в скобке должно быть (х+2) т.е. х двигаем влевоn=3 => после скобки +3получаем ответ:

у = -(х + 2)^2 + 3