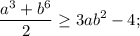
Вспоминаем неравенство Коши
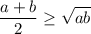
Применяем:
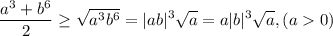
Покажем, что правое выражение здесь не меньше правого выражения в исходном неравенстве, тогда правое выражение в исходном неравенстве тем более будет не меньше, чем левое в исходном.
Это как если надо доказать, что a>b, мы доказали, что при a>c выполняется c>b, то точно a>b (транзитивность неравенств).
Делаем это:
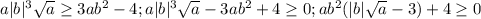
Это неравенство аналогично неравенству 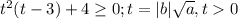
Чтобы решить это неравенство, надо найти нули функции
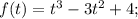 , здесь сумма коэффициентов при нечетных степенях (1) равна сумме коэффициентов при нечетных степенях (-3+4=1), значит, t=-1 - корень. Поделив уголком на t+1 или по схеме Горнера, получим разложение
, здесь сумма коэффициентов при нечетных степенях (1) равна сумме коэффициентов при нечетных степенях (-3+4=1), значит, t=-1 - корень. Поделив уголком на t+1 или по схеме Горнера, получим разложение 
Теперь можно решать неравенство, при этом по методу интервалов, так как при t везде коэффициент равен 1, в самом правом промежутке будет "+", а в остальных случаях при переходе через нули будет чередоваться, кроме нулей четности, как здесь t=2 (2-я степень при скобке), знаки будут - + +
Тогда ![(t+1)(t-2)^2\geq 0 \Rightarrow t \in[-1;2]\cup[2;+\infty) \Rightarrow t \in [-1;+\infty)](/tpl/images/0725/1584/edbb8.png)
Но мы рассматриваем только t>0, а там везде неравенство выполняется, значит, выполняется и неравенство 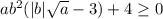 , то есть
, то есть 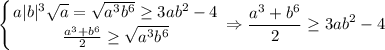
Что и требовалось доказать (естественно, неравенство справедливо по условию с ограничением a>0)
Решение
Через вершину B проведем прямую, параллельную AC, продлим медиану AА₁ до пересечения с этой прямой в точке T.
Из равенства треугольников А₁BT и A А₁C (по стороне и двум прилежащим углам: B А₁ = А₁C, т. к. A А₁ — медиана,
∠B А₁T = ∠A А₁C — вертикальные, ∠ А₁BT = ∠ А₁CA — накрест лежащие при параллельных прямых AC, BT и секущей BC) следует, что BT = AC и A А₁ = KT. Из подобия треугольников
AML и MBT (по двум углам: ∠MAL = ∠BTА₁,
∠ALB = ∠LBT — накрест лежащие при параллельных
прямых AC, BT и секущих BL, AT) следует,
что AL : BT = AL : AC = AM : MT. Так как АА₁ = А₁T,
то AM : MT = 1 : 7.
Тогда AL : AC = 1 : 7, а AL : LC = 1 : 6.
решение во вкладыше
Пусть первоначальная стоимость товара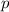 . После увеличения новая цена станет
. После увеличения новая цена станет 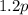 , после снижения –
, после снижения – 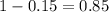 от повышенной цены, то есть
от повышенной цены, то есть 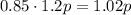 .
.
По условию конечная цена равна 102 рубля, поэтому
ответ. Первоначальная стоимость товара равна 100 рублей.