раскрывать каждый модуль 2 раза-получится 2^3=8 комбинаций
"+"-выражение в модуле ≥0, "-"-меньше 0
1)+++-все три выражения в модулях ≥0
5-x≥0;x≤5
x+1≥0;x≥-1
x-2≥0;x≥2
общий интервал тогда x=[2;5]
5-x-(x+1)=x-2; 5-x-x-1-x+2=0;6=3x;x=2-подходит выбранному интервалу
2)---
5-x<0; x>5
x+1<0;x<-1
x-2<0;x<2
общего интервала нет, значит и решений тоже
3)+--
x≤5;x<-1;x<2; x=(-∞;-1)
5-x-(-x-1)=-(x-2); 5-x+x+1+x-2=0;x=-4-подходит указанному интервалу
4)++-
x≤5;x≥-1;x<2; x=[-1;2)
5-x-(x+1)=2-x;5-x-x-1+x-2=0;2=x-не подходит интервалу
5)-+-
x>5;x≥-1;x<2; x=∅
6)-++
x>5;x≥-1;x≥2;x=(5;+∞)
x-5-(x+1)=x-2;x-5-x-1-x+2=0;-4=x-не подходит интервалу
7)--+
x>5;x<-1;x≥2;x=∅
8)---
x>5;x<-1;x<2;x=∅
Итого ответ x=-4;2
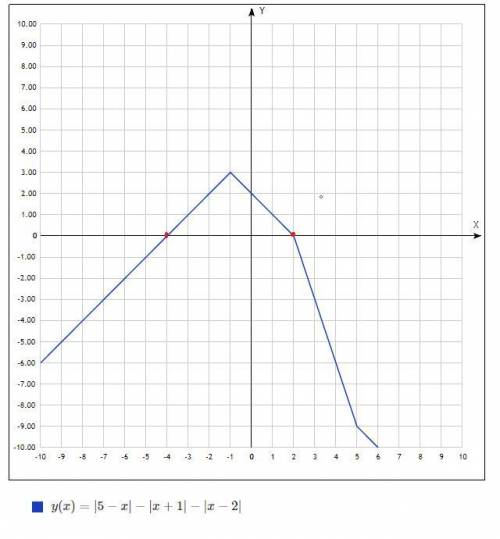
Объяснение:
Наибольшее и наименьшее значения - это экстремумы.
Это точки, в которых производная равна 0.
f(x) = 1/3*x^3 + 3/2*x^2 - 10x + 4
f ' (x) = x^2 + 3x - 10 = 0
(x+5)(x-2) = 0
x1 = -5; f(-5) = 1/3*(-125) + 3/2*25 - 10(-5) + 4 = -125/3 + 75/2 + 50 + 4 =
= -41 2/3 + 37 1/2 + 54 = (54+37-41) + (1/2-2/3) = 50 - 1/6 = 49 5/6.
x2 = 2; f(2) = 1/3*8 + 3/2*4 - 10*2 + 4 = 8/3 + 6 - 20 + 4 = 2 2/3 - 10 = -7 1/3.
Ясно, что f(-5) = 49 5/6 - максимум, а f(2) = -7 1/3 - минимум.