Пусть, для определённости, d>=c>=b>=a. Тогда всю дробь можно переписать в виде:
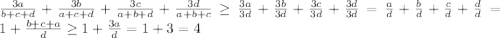
Что и требовалось доказать.
Пояснение: Выражение после первого знака неравенства получается, если взять наименьший знаменатель, а это d+d+d=3d.
Выражение после второго знака неравенства получается оттого, что мы берём наибольший числитель(то есть b+c+a=a+a+a=3a).
Выражение после третьего знака неравенства справедливо так как a>=d, то есть a/d>=1. Отсюда 3*(a/d)>=1*3=3
P.S. Если что-то непонятно, то не стесняйся спрашивать)
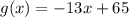. Найдем значение 
, при котором функция будет равна 
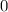. Для этого приравняем саму функцию к :
.
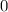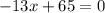
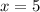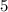данная функция перескает ось абсцисс (OX). Так как у функции угловой коэффициент отрицательный (число -13), следует заключение, что функция убывает на всей области определения. Так как это линейная функция, то область определения у неё, вся числовая прямая. Отсюда следует, что функия - убывающая!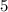. Так как функция убывает, то отсюда получаем:
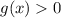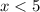
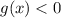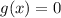при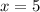 
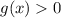при 
.
при 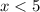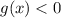при при 
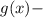убывающая
Объяснение:
(n+3)(n-3)(n-3)=(n²-9)(n-3)=n³-3n²-9n+27
n³-3n²-9n+27 n³(1-(3/n)-(9/n²)+(27/n³))
lim = =
n->∞ 3n³+7n+8 n³(3+(7/n²)+(8/n³))
'все дроби с n в знаменателе стремятся к 0, n³ сокращаем
=1/3