Пусть x- количество лет старшего брата и он старше младшего брата на y лет . Тогда младшему брату (x-y) лет
Когда старшему брату было (x-y) лет, то младшему было (x-y)-y=x-2y лет
Из условия задачи имеем уравнение
x-y=3*(x-2y)
Когда младшему брату будет x лет, старшему будет x+y лет
Составляем второе уравнение
x+(x+y)=60
Имеем систему
x-y=3x-6y
2x+y=60
2x-5y=0
2x+y=60
Из второго уравнения вычтем первое
6y=60
y=10 - разность в годах
2x+y=60 2x=60-y=50 x=25
То есть старшему брату 25 лет, а младшему 25-10=15 лет
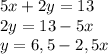
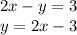
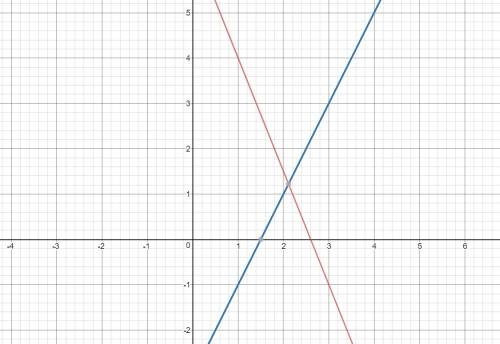
v₁ = 3км/час, v₂ = 5км/час
Объяснение:
1час15 мин = 75мин
1час = 60 мин
v₁ - скорость 1-ого пешехода
v₂ - скорость 2-ого
1) 1-е уравнение:
75(v₁ + v₂) = 10
2)
Т.к 1-ый пешеход вышел на 40мин раньше, то, если до встречи 2-ой пешеход шёл 1час = 60мин., то первый на 40мин. больше:
40мин + 60мин= 100мин. Получаем 2-е уравнение:
100v₁ + 60₂ = 10
3) Решаем систему (методом сложения):
{ 75v₁ + 75v₂ = 10 | * (-2)
{100v₁ + 60v₂ = 10 | * 2,5
{ -150v₁ - 150v₂ = 20
{ 250v₁ + 150v₂ = 25
100v₁ = 5
v₁ = 5/100 = 0,05 (км/мин) = 3км/час - скорость 1-ого пешехода.
Из 2-ого уравнения находим v₂ (км/мин), подставляя в него значение
v₁ =0,05км/мин:
100v₁ + 60v₂ = 10 → 60v₂ = 10 - 100*0,05 → 60v₂ = 5
v₂ = 5/60 = 1/12 (км/мин) = 5 км/час - скорость 2-ого пешехода