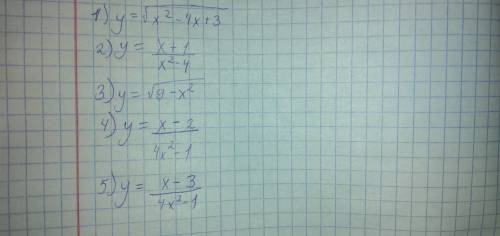
![1)\ \ y=\sqrt{x^2-4x+3}\\\\OOF:\ \ x^2-4x+3\geq 0\ \ ,\ \ (x-1)(x-3)\geq 0\ \ ,\\\\znaki:\ \ +++[\, 1\, ]---[\, 3\, ]+++\\\\x\in (-\infty ;\ 1\ ]\cup [\ 3\ ;+\infty \, )\\\\\\2)\ \ y=\dfrac{x+1}{x^2-4}\\\\OOF:\ \ x^2-4\ne 0\ \ ,\ \ \ (x-2)(x+2)\ne 0\ \ ,\ \ x\ne -2\ ,\ \ x\ne 2\\\\x\in (-\infty ;-2)\cup (-2\, ;\, 2\, )\cup (\ 2\, ;+\infty \, )\\\\\\3)\ \ y=\sqrt{9-x^2}\\\\OOF:\ \ 9-x^2\geq 0\ \ ,\ \ \ (3-x)(3+x)\geq 0\ \ ,\ \ (x-3)(x+3)\leq 0\ \ ,\\\\znaki:\ \+++[-3\, ]---[\, 3\, ]+++\\\\x\in [-3\ ;\ 3\ ]](/tpl/images/2006/9375/f8990.png)
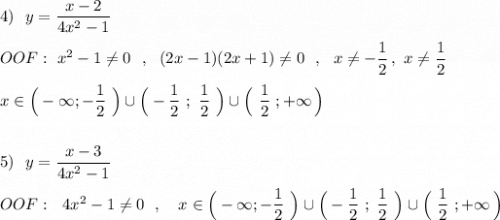
Сначала ОДЗ:5х-4>=0,х>=0,83х+1>=0,х>=-1/32х-1>=0,х>=0,5...берем "больше большего",получаем х>=0,8
sqrt(5x-4)+sqrt(2x-1)= sqrt(3x+1)
5x-4+2x-1+2*sqrt((5x-4)(2x-1)) =3x+1
4*(5x-4)(2x-1) = (6-4х)^2
4(10х^2-13x+4)=36-48x+16x^2
40x^2-52x+16=16x^2-48x+36
24x^2-4x-20=0
6x^2-x-5=0
D=1-4*6*(-5)=121... sqrt(121)=11
x1,2=(1+/-11)/12
x1=1,х2=-5/6...
по ОДЗ исключаем 2-й корень,ответ х=1...при возведении в квадрат могут появиться посторонние корни,поэтому делаем проверку,т.е.,подставляем х=1 в исх.ур-е...всё сходится,поэтому оконч. ответ х=1.