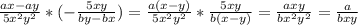Решение Пусть х км/ч - скорость второго пешехода. Тогда скорость первого - (х+1) км/ч. Так как встретились пешеходы в 9 км от пункта А, путь первого составил 9 км, а путь второго - 10 км. Значит, второй пешеход провел в пути (10/х) часов, а первый (9/(х+1)+0,5) часов, полчаса из которых потратил на остановку. Составим равнение: 10/x = 9/(x + 1) + 1/2 10/x = (18 + x + 1)/([2*(x + 1)] 20x + 20 = 18x + x² + x x² – x – 20 = 0 x₁ = - 4 не удовлетворяет условию задачи x₂ = 5 5 (км/ч) - скорость второго пешехода 1) 5 + 1 = 6 (км/ч) - скорость первого пешехода ответ: 6 км/ч ; 5 км/ч.
1)sinА^2+cosA^2= 1 Тогда cos(A) =√ 1-sinA^2= √1( 2/7)^2=√1-4/49=√45/49=√45/7=√9*√5/7=3√5/7 Вычислим тангенс, зная, что тангенсом острого угла называется отношение синуса угла к его косинусу. tg (A) =2/7 : 3√5/7=2*7/3√5*7=2/3√5 ctgA=cosa/sina=3√5/7/2/7=3√5/2 2)a) (sina+cos)^2+(sina-cosa)^2= =sin^2a+2sinacosa+cos^a+sin^2a-2sinacosa+cosa= =2sin^2a+2cos^2a=2 б) cos²α- cos⁴α+sin⁴α=cos²α(1- cos²α)+sin⁴α=cos²α·sin²α+sin⁴α
( sin²α=1-cos²α)
=sin²α(cos²α+sin²α)=
(sin²α+cos²α= 1)
=sin²α В) 1-cos^2a/1-sin^2a=sin^2a/cos^2a=tga 3)sin>0 cos<0 tg,ctg<0 750=2*360+30-1 2 полных оборота и поворот на 30 градусов 1 четверть в ней sin,cos,tg,ctg>0
Объяснение:
А)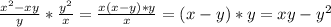
Б)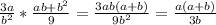
В)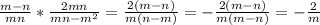
Г)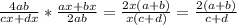
Д)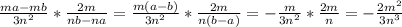
Е)