Объяснение: 2x²-8x+c = 0.
Имеем квадратное уравнение, где с - некоторое произвольное число (параметр), поэтому при разных значениях с уравнение может как иметь корни, так и не иметь. Поэтому нужно решить уравнения для всех возможных значений с.
Найдем дискриминант: 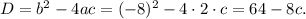
Рассмотрим 3 различных случая:
1) D < 0. Если D < 0, то уравнение не имеет решений. Найдем значения с, при которых дискриминант отрицателен: 64 - 8c < 0; 8c > 64 ⇔ c > 8. При таких значениях с корней у нас не будет вообще.
2) D = 0. Если D = 0, то уравнение имеет единственное решение: 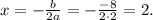 Найдем значение с, при котором дискриминант равен 0: 64 - 8c = 8 ⇔ c = 8. При таком значении параметра имеем один корень - х = 2.
Найдем значение с, при котором дискриминант равен 0: 64 - 8c = 8 ⇔ c = 8. При таком значении параметра имеем один корень - х = 2.
3) D > 0. Если D > 0, то уравнение имеет два различных корня, которые находятся по общей формуле: 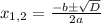 . Выразим каждый из корней:
. Выразим каждый из корней:
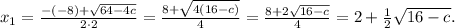
Аналогично 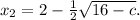
Найдем значения с, при которых дискриминант положителен: 64 - 8с > 0; 8с < 64 ⇔ c < 8. При таких значениях параметра у нас будут два корня: 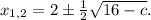
ОТВЕТ: если с < 8, то 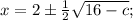 если с = 8, то х = 2; если с > 8, то корней нет.
если с = 8, то х = 2; если с > 8, то корней нет.
Відповідь:
Время, проведенное в пути равно 1 час 36 минут.
Пояснення:
Трофим до места прокола ехал 15 минут, а Трифон после прокола шел 1 час, преодолев такое же расстояние. Скорость пешего хода в три раза меньше скорости езды на велосипеде. Значит Трифон проехал бы это расстояние за 1 час / 3 = 20 минут.
Значит скорость Трифона (У) составляет 15 / 20 = 3/4 от скорости Трофима (Х).
У = 0,75Х
Т - время, проведенное в дороге.
0,25 × 3Х + (Т - 0,25) × Х = 1 × У + (Т - 1) × 3У
0,75Х + ТХ - 0,25Х = 0,75Х + 3×0,75ТХ - 3×0,75Х
0,5Х + ТХ = 2,25ТХ - 1,5Х
2Х = 1,25ТХ
Т = 2Х / 1,25Х = 2 / 1,25 = 1,6 часа. = 1 час 36 минут - время в пути.
Проверка.
1ч. 36м. - 15м. = 1ч. 21 м. - Трофим шел пешком.
1ч. 36м. - 1ч. = 36м. - Трифон ехал на велосипеде.
15м. × 3Х + 81м. × Х = 60 × У + 36 × 3У
45м. × Х + 81м. × Х = 60 × У + 108 × У
126м. × Х = 168м. × У = 168м. × 3 / 4 × Х
126м. × Х = 126м. × Х