Введем функции и . Про вторую сразу скажем, что , но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это при или . Тогда наименьшее значение этой функции будет равно .
Теперь разберемся с . У нас есть квадратный корень, поэтому все значения функции точно . Но и здесь мы идем дальше. Поменяем временно на букву . Тогда будет . Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное при , откуда .
Наибольшее значение равно и достигается при . Наименьшее значение равно и достигается при или .
1) Боря берет конфеты по арифметической прогрессии: 1, 3, 5, ... a1(1) = 1; d1 = 2 Миша - тоже по арифметической прогрессии a2(1) = 2; d2 = 2 Всего Боря взял S1(n) = (2a1 + d(n-1))*n/2 = (2 + 2(n-1))*n/2 = (1 + n - 1)*n = n^2 = 60 7 < n < 8 Значит, n = 7, предпоследний раз Боря взял a1(7) = 1 + 2*6 = 13. И у Бори получилось S1(7) = 7^2 = 49 конфет. Но мы знаем, что всего он взял 60 конфет. Значит, в последний раз 11. Миша последний раз взял 14. Это тоже 7-ой раз. Всего Миша взял S2(7) = (2*2 + 2*6)*7/2 = 2*8*7/2 = 56 Всего конфет было 60 + 56 = 116
2) 231 = 3*7*11 На каждом этаже квартир больше 2, но меньше 7, то есть 3. Допустим, в доме 7 этажей. Тогда в одном подъезде 3*7 = 21 квартира. Квартира номер 42 - последняя во 2 подъезде. Квартир с номерами больше 42 во 2 подъезде нет. Значит, в доме 11 этажей. Тогда в одном подъезде 3*11 = 33 квартиры. Квартира номер 42 - последняя на 3 этаже.
1) Требуется определить наиболее распространенный размер мужской одежды , для этой цели были взять размеры верхней одежды у мужчин и получены следующие данные : 52 , 46 , 52 , 48 , 48 , 44 , 48 , 50 , 48 , 50 , 48 , 42 , 48 , 47 , 48 , 52 , 50 , 48 , 56 ,48 , 54 , 46 , 54 , 50 . 2) Требуется определить наиболее распространенный размер женской обуви. Для этого были взяты размеры обуви у женщин . И результат был таким : 38, 38, 37, 39, 38, 37, 39, 40 ,36 , 38 , 38 , 37, 39, 35 , 37 , 39, 38 . 3) Было зарегистрированно число предметов , покупаемых в универсаме несколькими покупателями : 5, 4 , 3 ,7 , 4 , 8 , 6 ,3 , 3 , 12 , 1, 3 . Расположите в порядке возрастания и определите количество групп . 4) при подсчёте количества спичек в 20 коробках была составлена таблица: число спичек : 47 48 49 50 51 число коробок :2 . 1 .. 2 .. 12 .3
(см. объяснение)
Объяснение:
Введем функции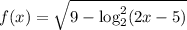 и
и  . Про вторую сразу скажем, что
. Про вторую сразу скажем, что 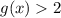 , но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это
, но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это  при
при 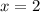 или
или 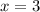 . Тогда наименьшее значение этой функции будет равно
. Тогда наименьшее значение этой функции будет равно 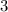 .
.
Теперь разберемся с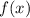 . У нас есть квадратный корень, поэтому все значения функции точно
. У нас есть квадратный корень, поэтому все значения функции точно 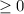 . Но и здесь мы идем дальше. Поменяем временно
. Но и здесь мы идем дальше. Поменяем временно 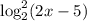 на букву
на букву 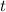 . Тогда будет
. Тогда будет 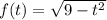 . Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное
. Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное 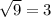 при
при 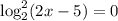 , откуда
, откуда 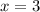 .
.
Наибольшее значение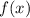 равно
равно 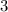 и достигается при
и достигается при 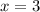 . Наименьшее значение
. Наименьшее значение 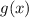 равно
равно 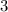 и достигается при
и достигается при 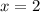 или
или 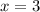 .
.
Тогда единственный корень исходного уравнения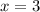 .
.
Уравнение решено!