Объяснение:
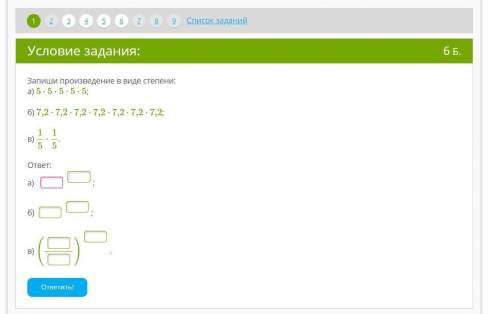
5^5
7,2^7
1/5^2
Набирал 12 страниц в час
Объяснение:
Пусть Наборщик планировал за час набрать x страниц. По условию, набирал (x+3) страницы за час. Тогда 180/х – запланированное время окончания работы, 180/(х+3) – время окончания работы в действительности и по условию составим уравнение:
180/х –180/(х+3)=5
180·(x+3)–180·x=5·x·(x+3)
180·(x+3–x)=5·x·(x+3)
5·x·(x+3)–540=0
5·x²+15·x–540=0 | :5
х²+3·x–108=0
D=3² –4·1·(–108)=9+432=441=21²
x₁=( –3 –21)/2= –24/2= –12<0 - не подходит
x₂=( –3 +21)/2= 18/2 = 9
Значит Наборщик планировал набирать 9 страниц в час, а набирал 9+3=12 страниц в час.
И всё же, ответ явился))
Возьмём поле, равное 1.
Пусть производительность первого - х п./ч, второго - у п./ч. Тогда их общая производительность равна х + у п./ч. Составим первое уравнение:
1 / (х + у) = 14
По другому условию составим второе уравнение:
7х + 14у = 2/3
Составим систему:
1 / (х + у) = 14
7х + 14у = 2/3
Выразим х + у из первого уравнения:
х + у = 1/14
7х + 14у = 2/3
Домножим обе части первого уравнения на 14:
14х + 14у = 1
7х + 14у = 2/3
Вычтем из левой части первого уравнения левую часть второго, то же самое с правыми частями:
(14х + 14у) - (7х + 14у) = 1 - 2/3
14х + 14у - 7х - 14у = 1/3
7х = 1/3
х = 1/21 п./ч - производительность первого тракториста
Выразим у из уравнения х + у = 1/14:
у = 1/14 - х
Подставим значение х:
у = 1/14 - 1/21
у = 3/42 - 2/42
у = 1/42 п./ч - производительность второго тракториста
Теперь узнаем, за сколько часов каждый тракторист может вспахать поле самостоятельно.
Первый тракторист: 1 : 1/21 = 1 × 21 = 21 ч
Второй тракторист: 1 : 1/42 = 1 × 42 = 42 ч
ответ: первый тракторист за 21 ч, второй за 42 ч.
Решение смотри на фотографии.