Question

Найдите произведение корней уравнения

Answer 1

$a. \ 0$

Объяснение:

$D(x): \displaystyle \left \{ {{-12x \geq 0} \atop {-3x \geq 0}} \right. \Leftrightarrow \left \{ {{x \leq 0} \atop {x \leq 0}} \right. \Leftrightarrow x \leq 0;$

$\dfrac{3^{\sqrt{-12x}}+3}{4}=3^{\sqrt{-3x}} \ ;$

$3^{\sqrt{-3x \cdot 4}}+3=4 \cdot 3^{\sqrt{-3x}} \ ;$

$3^{\sqrt{-3x} \cdot \sqrt{4}}+3=4 \cdot 3^{\sqrt{-3x}} \ ;$

$3^{\sqrt{-3x} \cdot 2}+3=4 \cdot 3^{\sqrt{-3x}} \ ;$

$(3^{\sqrt{-3x}})^{2}-4 \cdot 3^{\sqrt{-3x}}+3=0;$

Введём замену:

$t=3^{\sqrt{-3x}} \ ;$

Перепишем уравнение с учётом замены:

$t^{2}-4t+3=0;$

Решим уравнение при теоремы Виета:

$\displaystyle \left \{ {{t_{1}+t_{2}=-(-4)} \atop {t_{1} \cdot t_{2}=3}} \right. \Leftrightarrow \left \{ {{t_{1}+t_{2}=4} \atop {t_{1} \cdot t_{2}=3}} \right. \Leftrightarrow \left \{ {{t_{1}=1} \atop {t_{2}=3}} \right. ;$

Вернёмся к замене:

$3^{\sqrt{-3x}}=1 \quad \vee \quad 3^{\sqrt{-3x}}=3;$

$3^{\sqrt{-3x}}=3^{0} \quad \vee \quad 3^{\sqrt{-3x}}=3^{1};$

$\sqrt{-3x}=0 \quad \vee \quad \sqrt{-3x}=1;$

$-3x=0 \quad \vee \quad -3x=1;$

$x=0 \quad \vee \quad x=-\dfrac{1}{3};$

Оба корня удовлетворяют ОДЗ.

Произведение корней:

$0 \cdot \bigg (-\dfrac{1}{3} \bigg )=0;$

Answer 2

0

Объяснение:

Область допустимых значений (ОДЗ):

$\begin{cases} -12x\geq 0\\-3x\geq 0 \end{cases}\\x\leq 0$

$\frac{3^{\sqrt{-12x} }+3}{4}= 3^{\sqrt{-3x} }\\\frac{3^{\sqrt{4*(-3x)} }+3}{4}= 3^{\sqrt{-3x} }\\\frac{3^{2\sqrt{-3x} }+3}{4}= 3^{\sqrt{-3x} }\\\frac{(3^{\sqrt{-3x} })^2+3}{4}= 3^{\sqrt{-3x} }\\3^{\sqrt{-3x} }=t, \; t0\\\frac{t^2+3}{4}=t\\t^2+3=4t\\t^2-4t+3=0$

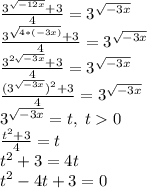
По теореме Виета

$\begin{cases} t_1+t_2=4\\t_1*t_2=3 \end{cases}\\\begin{cases} t_1=1\\t_2=3 \end{cases}$

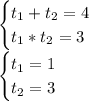
Возможны два случая.

Первый:

$3^{\sqrt{-3x} }=1\\3^{\sqrt{-3x} }=3^0\\\sqrt{-3x}=0\\-3x=0\\x=0$

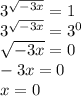
Поскольку среди корней есть ноль, их произведение будет нулевым, какими бы не были остальные корни. Поэтому дальше их можно не искать, но я все же закончу решение.

Второй:

$3^{\sqrt{-3x} }=3\\3^{\sqrt{-3x} }=3^1\\\sqrt{-3x}=1\\-3x=1\\x=-\frac{1}{3}$

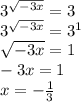
Оба корня — -1/3 и 0 — входят в ОДЗ, их произведение — 0.